コンデンサーの充放電特性

実験番号:UE3030105
コンデンサーは直流電流を通しませんがせんが,交流電流は流れます。この現象を理解する第一歩としてコンデンサーへの充放電の性質を調べます。コンデンサー充電時の電圧特性を,外部電圧を印加した瞬間からコンデンサー両端の電圧を経時的に測定しグラフ化します。放電時の電圧特性も同様に,放電開始時からの電圧を測定していきます。グラフからコンデンサー回路の時定数と呼ばれる定数を求めることができます。
実験の手順
- コンデンサー充電時の電圧変化を時間を追って測定します
- コンデンサー放電時の電圧変化を時間を追って測定します
- 測定結果からコンデンサーの電気容量と接続されている抵抗値を決定します
実験に必要な機器
- U10800-115:充放電特性実験器 ×1
- U333106:コンデンサー・1000 µF/35V ×1
- U333030:抵抗・10 kΩ/0.5W ×1
- U11806:デジタルマルチメーター・P1035 ×1
実験解説書
英語版 実験手順書 ダウンロード(参考,一部取り扱いのない製品も含まれています)
基本原理
コンデンサーの基本構造は,2枚の電極が絶縁体(誘電体)を挟んだものです。その為,電極間を電荷が移動することはありません。これが直流を通さない理由ですが,コンデンサーに印加する電圧を変えたときには,コンデンサーの充放電(電荷の蓄積・放出)が起こります。誘電体内で電荷が通過することはありませんが,コンデンサー電極と外部で電荷のやりとりがあるので,回路としては電流が流れます。
この現象を調べるため,コンデンサーの充放電特性,充電時と放電時の電圧が時間的にどのように変化するかを測定します。この過程で時定数という回路の重要なパラメータが表れます。
理想的なコンデンサーが充放電するときの電圧変化は計算で示すことができます。しかし微分方程式を解く必要があることから,最初に定性的に考えてみます。
コンデンサーに電荷がある状態で一定電圧を印加して充電することを考えると,充電のために送られる電荷には先にコンデンサーにある電荷による電場から斥力を受けます。(充電するときには,印加した電圧による電場がそれに打ち勝っている状態です。)電荷がコンデンサーに蓄えられるほど斥力を生む電場は強くなり,充電するスピードは遅くなります。このことからコンデンサーに充電するときのコンデンサー両端電圧変化は直線的ではなく,段々と変化が小さくなります。(コンデンサーで両端電圧が蓄えられた電荷に比例することに注意しましょう。)コンデンサーが空(=電荷が無い状態)のときの電圧変化が最大になります。
放電のときも同じ考え方で,放電を始めた瞬間の電圧変化が一番大きくなることが分かります。
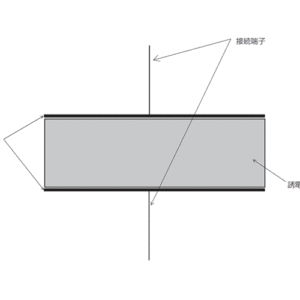
コンデンサーの充放電時の等価回路は図1のようになります。ここで![]() とキルヒホッフの法則より充電時・放電時には次のようになります。
とキルヒホッフの法則より充電時・放電時には次のようになります。
充電時

この型の微分方程式は![]() の解を持ちます。t=0でQ=0,t=∞でQ=C・U0より
の解を持ちます。t=0でQ=0,t=∞でQ=C・U0より

放電時

こちらは単純な![]() の解であり,t=0でQ=C・U0,t=∞でQ=0より
の解であり,t=0でQ=C・U0,t=∞でQ=0より

となります。
充放電特性を決める抵抗値Rとコンデンサーの静電容量Cの積を時定数 τ と呼びます。

またこれらの式から

実験器では外部印加電圧(U0)は10V固定です。機器はコンパレータ(比較器)を内蔵しており,ダイヤルで設定した基準電圧Vcになるとタイマーがストップします。Vcを0.5Vから(放電時は9.5Vから)順次,時間を測定しグラフにします。
装置内蔵の抵抗・コンデンサーの組み合わせだけでなく,4mm安全ソケット(4mmバナナプラグが嵌合)に抵抗・コンデンサーを接続することで,種々の時定数での測定が可能です。
評価
t=3τ=3RCで充放電が95%完了することより,RCいずれかが既知であれば,残りの値を充放電特性を測定することで決定できます。これを使い,装置内部の抵抗・コンデンサーの値を決定します。
最初に実験器の回路選択スイッチはEXTERNにし,適当な外部抵抗(~10kΩ)とコンデンサー(~1000μF)を実験器に接続します。この回路の充電もしくは放電の3τを測定します。通常,抵抗の公差の方が小さいので抵抗値を既知として接続したコンデンサー容量Cexを計算します。(もしくは,マルチメーターで抵抗を測定しておきます。)
(3)
次にスイッチをINTERN3にし,外部コンデンサーを接続(内蔵コンデンサーと並列になります)したときと接続しないとき,それぞれのτを3τ⇒95%から測定します(時定数をそれぞれτ1,τ2とします)。内蔵抵抗Rin3と内蔵コンデンサーCinの2つが未知ですが,τ1,τ2の比を取ることで未知抵抗Rin3が消えます。
(4)
ここで得たCinを元に内蔵抵抗1~3(INTERN1~INTERN3)の値が3τを測定することで求められます。
参考資料
-
図1:コンデンサー概念図
-
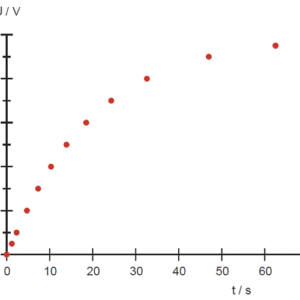
図2:実験器内蔵のRCによる充電時電圧 (R~10kΩ,C~2000μF)
-
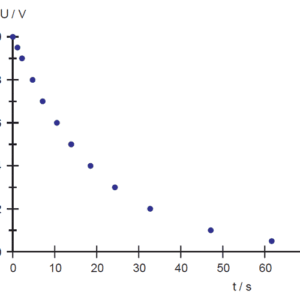
図3:実験器内蔵のRCによる放電時電圧 (R~10kΩ,C~2000μF)