ソレノイドの磁束密度

実験番号:UE3030500
磁場は電流(電荷の動き)によって作られます。静電荷のクーロンの法則に対応するのが,電流素片が作る静磁場を記述したビオ・サバールの法則となります。ソレノイドと呼ばれる長いコイル内部の磁場は,径に依存せず単位長さあたりの巻数と電流値にのみ依存します。この事をビオ・サバールの法則から計算で示し,その後,径の異なる円筒コイルや単位長さあたりの巻数を変えたコイルで内部磁場を実測し,検証します。
実験の手順
- 円筒型コイルの内部磁場(磁束密度)を,径の異なる2つのコイルで電流値を変えながら測定します。
- コイルの単位長さあたりの巻数を変えて内部の磁束密度を測定します。
実験に必要な機器
- U12252:磁場コイル・120回巻・100mm ×1
- U12253:磁場コイル・120回巻・120mm ×1
- U8496175:巻数可変コイル ×1
- U8496150:アクリルスタンド ×1
- U331101-115:テスラメーター ×1
- U13801:低電圧用リード線・75cm・15本セット ×1
- U13265:支柱用台座 ×1
- U15001:ステンレス鋼製支柱・25cm ×1
- U13255:角型ムッフ ×1
- U13261:万能クランプ ×1
- 直流電源(10V/20A) ×1 (別途ご用意ください)
実験解説書
英語版 実験手順書 ダウンロード(参考,一部取り扱いのない製品も含まれています)
基本原理
磁場は電流(電荷の動き)によって作られます。静電荷のクーロンの法則に対応するのが,電流素片が作る静磁場を記述したビオ・サバールの法則となります。実際の磁場は電流素片が作る磁場を足し合わせる(積分する)ことで計算できます。これより磁場は電流の流れる経路(空間形状)にも依存しますが,単純な電流経路以外では計算は複雑となります。長いコイル(ソレノイド)内部の磁場は簡単に計算できる例の1つです。この計算からソレノイド内部の磁場は径に依存せず,単位長さあたりの巻数と電流値にのみ依存する事が分かります。
ビオ・サバールの法則は静磁場を計算する手法で,次の式で表わされます。

ここでμ_0 は真空の透磁率で,![]()
定電流Iが流れるとすれば![]() を
を![]() で置き換えて,次式になります。
で置き換えて,次式になります。

ソレノイドの内部磁場を計算するために,まず半径Rの円電流が作る磁場を計算します。(図1)

ここでの計算は,円の中心を通り円に垂直なx軸上の磁場を与えています。 円の中心では,上式でx=0とおきます。

無限に長いソレノイドの単位長さあたりの巻数をnとすると,長さdxの巻数はn⋅dxとなります。よってそこを流れる電流はI⋅n⋅dx になります。ビオ・サバールの法則を全空間について積分すると,電流密度が0(電流が流れていない空間)ではds=0なので結局()をxについて積分すれば良い事が分かります。

積分を計算するのに次の変数変換を行います。


有限長のソレノイド(長さL,巻数N)ではn=N/Lなので上式を,

とも書けます。無限長のソレノイドの式を有限長に適応する場合の制限は後で触れます。
実験は径の異なる2つのコイルで電流を変えて内部磁場をテスラメーターで測定します。(図1) この結果からソレノイド内部磁場は径によらず,電流値に比例していることが分かります。また径によらないことから,形も円筒である必要がない事も分かります。 次に単位長さあたりの巻数を変えて,同様に内部磁場を測定します。(図2,図3)
評価
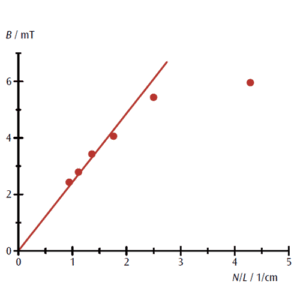
全ての測定結果から,ソレノイドの内部磁場は電流値に比例することが言えます。また図4よりコイル直径と長さの比が1:3近傍(L=17cm)までは内部磁場と単位長さあたりの巻数が比例することも確認できます。コイル直径に対してコイル長さが短くなると,コイル端部の影響が無視できなくなるためです。ソレノイドの自己インダクタンスを計算する際の長岡係数のようにコイル径と長さの比がパラメータとなっていることが知られています。
参考
ビオ・サバールの法則は,静磁場を計算する上でアンペールの法則よりも自由度があり有用です。しかし,このときの電流素片は物理的に存在しません。(電荷の保存則が破れます。) 積分形式で全電流素片を積分する場合は物理的に存在しうる状態であり,静磁場を正 しく与えます。
参考資料
-
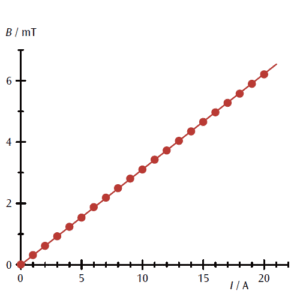
図1:コイルの内部磁束密度と電流のグラフ
-
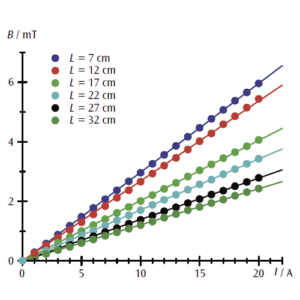
図2:Lを変えた場合の内部磁束密度と電流のグラフ
-
図3:単位長さあたりの巻数N/Lと磁束密度のグラフ(I=20A)