変動磁場による電磁誘導

実験番号:UE3040300
交流電流が流れる円筒形コイル内に N 回巻の閉じた導体ループを置くと,ループを貫く磁束の変化によって誘起電圧が発生します。この誘導起電圧は,導体ループの巻数や断面積の他に,磁場コイルを流れる交流電流の周波数,振幅,波形にも依存します。これらの依存関係を調べて,ファラデーの電磁誘導の法則を確認します。
実験の手順
- 誘導起電圧と磁場コイルを流れる電流の振幅 I0 と周波数fとの関係を測定します。
- 誘導起電圧の誘導コイルの巻数 N と断面積Aへの依存性を測定します。
- 誘導起電圧と磁場コイルを流れる電流の波形との関係を測定します。
実験に必要な機器
- U122501:誘導コイル・3本セット ×1
- U12253:磁場コイル・120回巻・120mm ×1
- U8496150:アクリルスタンド ×1
- U51004:抵抗器・1Ω ×1
- U8533600-115:関数発生器 ×1
- U11830:USBオシロスコープ2x25MHz ×1
- U11257:BNC-4mmプラグ変換ケーブル ×2
- U13812:プラグ付き安全リード線・75cm・2本セット ×2
- Windows PC ×1 (別途ご用意ください)
実験解説書
基本原理
N 回巻の閉じた導体ループを貫く磁束の変化によって,ループ内に誘起電圧が発生します。磁束の変化は,磁場に対する導体ループの面積を変えることや,交流電流が流れる磁場コイル内に導体ループを置くことなどで生じさせることができます。ファラデーの電磁誘導の法則によれば,磁束の時間変化率と誘導起電圧には以下の関係が成り立ちます。
(1)\[ U(t)=- \frac {d \phi (t)} {dt} \] 磁束密度Bが,面積 A の領域を垂直に通る場合,この面積 A を通る磁束Φは次式で与えられます。
(2)\[ \phi = B \cdot A \] ここで,B: 磁束密度。 よって式 (1) から,一定の面積AでN回巻のコイルであれば次の結果が得られます。
(3)\[ U(t) = – N \cdot A \cdot \frac { dB(t) } { dt } \] 磁場コイルをソレノイドとして扱うことで,導体ループ内には以下のような磁束密度が発生することが分かります。
(4)\[ B(t) = \mu_0 \cdot \frac { N_F} { l_F } \cdot I(t) \] ここで,μ0 = 4π∙10-7 N/A2: 真空透磁率, NF: 磁場コイルの巻数, lF: 磁場コイルの長さ, I(t): 磁場コイル内を流れる電流。以上の式から,誘導起電圧U(t)は磁場コイルを流れる変動電流I(t)を使って次のように書けます。
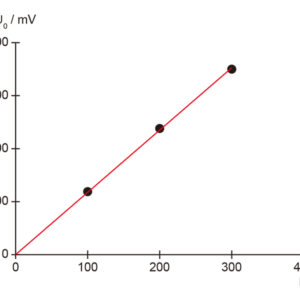
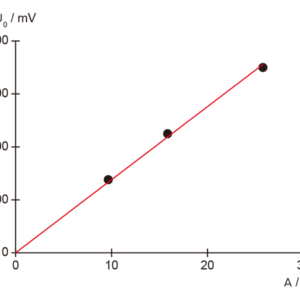
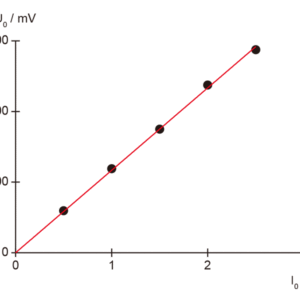
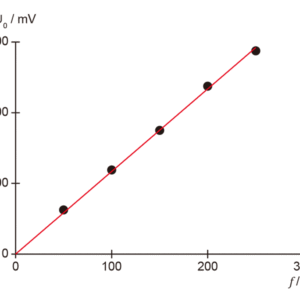
(5)\[ U(t) = – \mu_0 \cdot N \cdot A \cdot \frac { N_F } { l_F } \cdot \frac { dI(t) } { dt } \] 実験の測定はオシロスコープで行います。関数発生器を使って,磁場コイルに正弦波電圧を印加します。磁場コイルを流れる電流I(t)の振幅 I0 は,コイルと関数発生器との間に直列に接続された抵抗両端電圧から換算できます。 印加正弦波電圧の振幅・周波数を変えて誘起起電力U(t)を測定することで,U(t)の振幅 U0 が印加正弦波電圧の周波数 f と磁場コイル内を流れる電流の振幅 I0 に依存することが確かめられます。 また誘導コイルを変えて同様の測定を行い,誘導コイルの巻数Nと断面積Aに対する依存性を確認します。 最後に誘導コイルと印加電圧の周波数を一定に保ったまま,三角波及び矩形波を磁場コイルに流して,誘導起電圧と電流波形の関係を確かめます。 各実験結果はオシロスコープのスクリーンショットを保存すると良いでしょう。
評価
正弦波電流
\[ I(t) = I_0 \cdot \sin {(2 \pi \cdot f \cdot t)} \] に対して,誘起起電力U(t)は計算上次の式になります。
\[ U(t) = -U_0 \cdot \cos { (2 \pi \cdot f \cdot t) } \] ここで,
\[ U_0 = 2 \pi \cdot \mu_0 \cdot N \cdot A \cdot I_0 \cdot f \cdot \frac { N_F } { l_F } \] 安全上の注意)
1Ω抵抗の最大電力は4Wなので,これを超えない範囲の電力で実験を行ってください。
参考資料
正弦波電流による誘導起電圧の各ファクターへの依存性測定
-
巻数Nへの依存性
-
断面積Aへの依存性
-
一次側電流振幅I0への依存性
-
一次側電流振動数fへの依存性
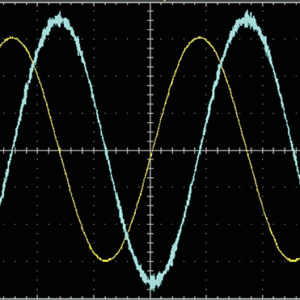
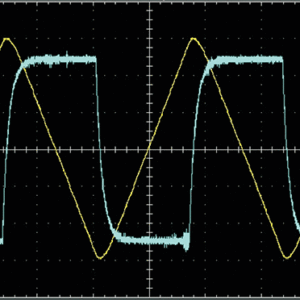
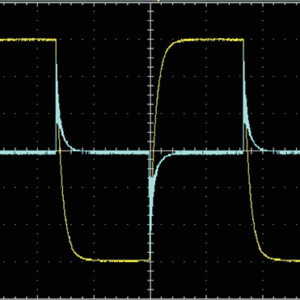
一次側電流波形(黄)と誘導起電圧波形(青)
-
正弦波
-
三角波
-
矩形波電流