変圧器の基礎

実験番号：UE3040500

交流の電圧を変える変圧器はファラデーの電磁誘導の法則を原理としています。良く知られた使用例として電力を遠方へ送る送電線があります。送電線では交流電圧を高くした状態（数十万ボルト）で遠距離へ送電しています。同じ電力を送るのに電圧を上げれば電流は小さくなり，送電時のジュール熱によるロスが小さくなるからです。本実験では二次側に負荷がない時とショートした時の変圧器の特性を測定します。また実験結果から，電力損失について検討します。

実験の手順

• 開放状態（オープン状態）の二次コイルの誘起電圧を，一次コイル印加電圧を変数として測定します。
• 二次コイルをショートさせたときの一次・二次それぞれのコイル電流を測定します。
• 電力損失について検討します。

実験に必要な機器

• U8497430：変圧器コイル・600巻・D型 ×1
• U8497440：変圧器コイル・1200巻・D型 ×1
• U8497180：変圧器鉄心・D型 ×1
• U138021：プラグ付き安全リード線・75cm・15本セット ×1
• 交流電源(20V/5A) ×1（別途ご用意ください）
• マルチメーター(AC電圧/電流測定可能なタイプ) ×1（別途ご用意ください）

お見積りフォーム

実験解説書

実験解説書 ダウンロード（PDF）

基本原理

交流変圧器はファラデーの電磁誘導の法則を原理としています。コイルを貫く磁束の変化率に比例し，変化を妨げるように電流を流すような起電力が発生する，というものです。また理想的な変圧器ではエネルギー損失0で電圧変換を行うとします。それらから単純な式で変圧された電圧を計算できます。

一次側コイル（コイル1）

• 巻数：\(N_1\)
• インダクタンス：\(L_1\)
• 電流：\(I_1\)
• 誘導起電力：\(U_{ind}\)
• 印加電圧：\(U_1\)

二次側コイル（コイル2）

• 巻数：\(N_2\)
• インダクタンス：\(L_2\)
• 電流：\(I_2\)
• 誘導起電力：\(U_2\)

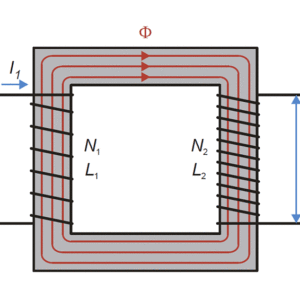
変圧器の原理を理解するために，理想的なコイルが2つの変圧器を考えます。それぞれのコイルのパラメーターを上記のように記載します（図1）。 また2つのコイルは閉じた鉄心に取り付けられているとし，巻線の巻き方は同じ向きとします。両コイルの巻線抵抗は0であるとします。

今，コイル2が無負荷（開放）状態を考えます。コイル1に電圧(U_1)を印加したときコイル2に発生する誘導起電力は次のように計算できます。コイル1に電流が流れるので鉄心内に磁束(Phi_1)が生じます。またコイル1は直流抵抗成分を持たないので(L_1)によるインピーダンスの電圧降下，つまりコイル1の逆起電力（＝コイル1の誘導起電力(U_{ind})）と(U_1)の和が0になります。

(1) \[ U_1+U_{ind}=0 \] \[ U_1=L_1\cdot \frac{dI_1} {dt} =-N_1\cdot \frac{d\Phi_1} {dt}=-U_{ind} \]

同じ大きさの磁束がコイル2を通っているので，コイル2の誘導起電力(U_2)は次のように書けます。

(2) \[ U_2=-N_2\cdot \frac{d\Phi_1} {dt} =\frac{N_2} {N_1}\cdot U_1 \] \[ \therefore \frac {U_2} {U_1} = \frac {N_2} {N_1} \]

ここでは2つのコイルの巻線の向きが同じなので負号が打ち消されましたが，巻線の向きが逆であれば負号が残ります。

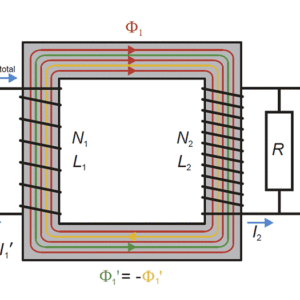
次にコイル2をショートした場合を考えます。ただし，電流を測定するために電流計を繋ぐ必要があり，電流計の微小な内部抵抗をRとします（図2）。

この時はコイル2に流れる電流(I_2)と(U_2)は(U_2=I_2cdot R)で結ばれます。(I_2)の作る磁束(Phi_1′)は元々の磁束(Phi_1)と逆向きに生じます。(U_1)は外部からの印加電圧で固定（影響を受けない）なので(1)式はそのまま成り立ちます。結果，(Phi_1′)を打ち消すためにコイル1は電流(I_1′)だけ増加します。

\[ N_2\cdot \Phi_1’=L_2\cdot I_2 \] \[ L_1\cdot I_1′ = N_1\cdot \Phi_1′ \] \[ I_1′ = \frac{1} {L_1} \cdot N_1 \cdot \Phi_1′ =\frac{N_1} {L_1} \cdot \frac{L_2} {N_2} \cdot I_2 =\frac{L_2} {L_1} \cdot \frac {1} {R}\cdot U_1 \]

この時に電力は2つのコイルをどの程度伝達されるかを見ます。コイル1への外部からの印加電圧(U_1)は周期的に変動しているとすれば，1周期の電力の平均がコイル1の消費電力(P_1)となります。

(3)\[ \begin{eqnarray*} P_1&=&\overline{I_{1(total)} \cdot U_1} = \frac{1} {T} \cdot \int_0^T{ I_{1(total)} \cdot U_1 \cdot dt}\\ &=&\frac{1} {T} \cdot \int_0^T{ \left( \left(I_1+I_1’\right) \cdot U_1 \right) \cdot dt} \end{eqnarray*} \]

一方，コイル2の消費電力は固定抵抗Rによるジュール熱ですから，こちらも1周期の平均は次のようになります。

\[ \begin{eqnarray*} P_2=\overline{{I_2} \cdot U_2}&=&\frac{1} {T} \cdot \int_0^T{ \frac{1} {R} \cdot U_2^2 \cdot dt}\\ &=&\frac{1} {T \cdot R} \cdot \int_0^T{ \left( \frac{N_2} {N_1} \cdot U_1 \right)^2 \cdot dt} \end{eqnarray*} \]

ここまでは電圧・電流の位相を考慮してきませんでしたが，全て同位相かは明らかではありません。自明ではありません。

それらを見る為に印加電圧を(U_1 = Ucdot sin{left(omega cdot tright)})として平均を計算してみます。（1）式から(I_1)は次のように計算できます。ここではt=0で外部電圧を印加し始めたとしています。

\[ U_1-L_1 \cdot \frac{dI_1}{dt}=0 \\ \frac{dI_1} {dt} = \frac{U_1} {L_1} =\frac{U} {L_1} \cdot \sin{\left(\omega \cdot t\right)} \\ I_1 = \frac{U} {L_1} \cdot \int {\sin{\left(\omega \cdot t\right)} \cdot dt} = – \frac{U}{\omega \cdot L_1}\cdot \cos{\left(\omega \cdot t \right)} = \frac{U}{\omega \cdot L_1} \cdot \sin{\left(\omega \cdot t – \frac {\pi} {2}\right)} \]

コイル2の誘起電圧(U_2)は，(2)式から明らかなように(U_1)と同位相です。またコイル2には固定抵抗しか接続されないため電圧の位相がそのまま電流の位相となります。これらを踏まえて電力の計算を進めます。(P_1)は（3）式から次のようになります。

(4) \[ \begin{eqnarray*} P_1&=&\frac{1} {T} \cdot \int_0^T{ \left( \left(I_1+I_1’\right) \cdot U_1 \right) \cdot dt} \\ &=&\frac{1}{T} \cdot \int_0^T {\left( -\frac{U}{\omega \cdot L_1} \cdot \cos{\left(\omega \cdot t \right)} + \frac{L_2}{L_1} \cdot \frac{1}{R}\cdot U \cdot \sin{\left(\omega \cdot t\right)} \right) \cdot U \cdot \sin{\left(\omega \cdot t \right)}\cdot dt } \\ &=&\frac{1}{R}\cdot \frac{L_2}{L_1}\cdot \frac{U^2}{2} \end{eqnarray*} \]

ここで三角関数の関係式を使っています。

同様に(P_2)次のとおりです。

(5) \[ \begin{eqnarray*} P_2&=&\frac{1} {T \cdot R} \cdot \int_0^T{ \left( \frac{N_2} {N_1} \cdot U_1 \right)^2 \cdot dt} \\ &=&\frac{1}{T \cdot R} \cdot \left( \frac{N_2}{N_1}\right)^2\cdot U^2\cdot \int_0^T\sin^2{\left( \omega \cdot t \right)}\cdot dt \\ &=&\frac{1}{R} \cdot \left( \frac{N_2}{N_1}\right)^2\cdot \frac{U^2}{2} \end{eqnarray*} \]

理想的なコイルのインダクタンス(L)は次式で表わされます。

\[ L=\frac{\mu \cdot N^2 \cdot S}{l} \]

ここで(mu)は透磁率，(l)はコイルの長さ，(S)はコイルの断面積です。これと（4）式，（5）式から，次のように一次側と二次側コイルの消費電力が等しい事が分かります。

\[ \begin{eqnarray*} P_1&=&\frac{1}{R}\cdot \frac{L_2}{L_1}\cdot \frac{U^2}{2} \\ &=&\frac{1}{R}\cdot \frac{\frac{\mu \cdot N_2^2\cdot S} {l}} {\frac{\mu \cdot N_1^2\cdot S} {l}} \cdot \frac{U^2}{2} \\ &=&\frac{1}{R} \cdot \left( \frac{N_2}{N_1}\right)^2\cdot \frac{U^2}{2} =P_2 \end{eqnarray*} \]

更にここから電流についても簡単な関係が成り立っていることが示せます。

(6) \[ P_1=\overline{I_{1(total)} \cdot U_1} = P_2 =\overline{{I_2} \cdot U_2} \]\[ \therefore \,\,\frac{I_2}{I_{1(total)}} = \frac{U_1} {U_2} = \frac{N_1}{N_2} \]

本実験は下記のように進めます。

1. 一次側コイルの巻線数を(N_1 = 600)，二次側巻線数を(N_2 = 1200)に設定します。
2. 二次側開放（オープン）の状態で一次側入力電圧0からを徐々に上げていき，その時の二次側コイル両端電圧を測定しグラフにします。この時の傾きを調べます。
3. 二次側コイルをマルチメーターを通じてショートさせ，一次側入力電圧を0から徐々に上げていきます。一次側・二次側電流値を測定しグラフにします。この時の傾きを調べます。
4. 時間があれば一次側・二次側コイル巻線数を変更し，上の実験を再度行います。この時の傾きを調べます。

評価

以下の測定は全て60Hzで行っています。

1），誘起電圧

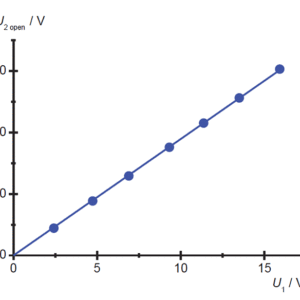
開放状態での誘起電圧測定は次のような結果になりました。

U1 [V]	U2_open [V]
2.42	4.43
4.74	8.84
6.9	12.92
9.32	17.59
11.37	21.52
13.5	25.63
15.92	30.32

グラフ2の傾きは約1.90となります。(1)式が表わす理想変圧器の誘起電圧は，\(\frac{N_2}{N_1} = 2\)でした。この違いの原因については後で検討します。

2），誘起電流

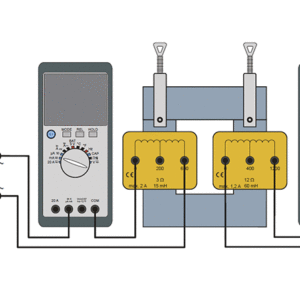
測定時の結線は下図の通りです。

短絡状態としていますが，先に検討したようにマルチメーター内部抵抗があるため，非常に小さな抵抗Rが二次側回路に入っています。

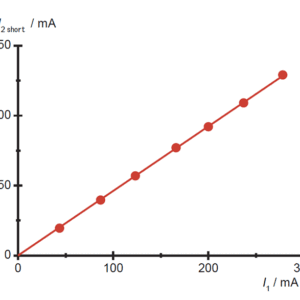
この時の測定結果は次のとおりです。

I1 [mA]	_sI_2hort [mA]
43.6	19.5
86.8	39.6
123.3	56.9
166	77
200	92
237	109
278	129

グラフの傾きは約0.46で，理想的な場合の(6)式，\(\frac{N_1}{N_2} = 0.5 \)とは一致していません。

こうした状況は測定の誤差だけではなく，元々現実のトランス（変圧器）には大きく分けて次のような損失があり，理想的な状態から外れているためです。

• 巻線の抵抗値は小さいが0ではないこと（銅損，抵抗による損失）
• 鉄心にはヒステリシスがあることと，鉄心内部で渦電流が発生すること（鉄損＝ヒステリシス損+渦電流損）
• 一次側コイルが作る磁束が全て二次側コイルを貫くのではないこと（漏洩磁束による損失）

それぞれの損失を具体的に測定することは難しいですが，実際に使用される変圧器では損失を少なくするための様々な工夫がなされています。