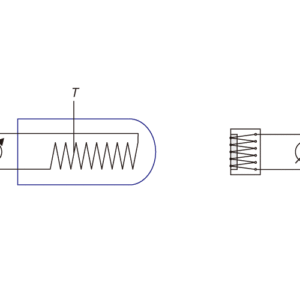
シュテファン＝ボルツマンの法則

実験番号：UE4050200

黒体放射（黒体輻射）の温度依存性は，シュテファン＝ボルツマンの法則によって表されます。これに類似した温度依存性は，タングステン・フィラメントを有する白熱電球からの，放射強度にも見られます。本実験では，モル型熱電対列を使って放射強度の相対値を測定し，この法則の検証をおこないます。フィラメントの温度は，フィラメントの抵抗値の温度依存性を利用して，4線式熱電対を使用することにより，非常に正確に求められます。

実験の手順

• タングステン・フィラメントを持つ白熱電球が発する光＝電磁波（熱放射）の，温度変化による相対強度を，モル型熱電対列を使って測定します。
• フィラメントの温度を計測するために，フィラメントの電気抵抗を測定します。
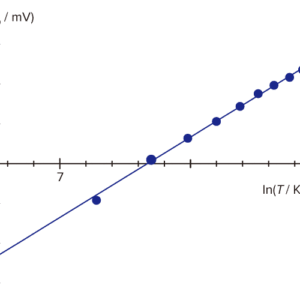
• 熱電対の読み取り値を，温度の関数として対数グラフに描き，得られた直線の傾きから，べき指数を求めます。

実験に必要な機器

• U8490050：黒体放射ランプ ×1
• U8441301：モル型熱電対列 ×1
• U11806：デジタルマルチメーター，P1035 ×3
• U13265：支柱用台座 ×2
• U138021：75cmプラグ付き安全リード線・15本セット ×1
• 直流電源(20V/5A) ×1 （別途ご用意ください）

お見積りフォーム

実験解説書

実験解説書 ダウンロード（PDF）

基本原理

物体からの熱放射の全強度とスペクトル分布は，その物体の温度とその表面の性質に依存しています。特定の波長と温度で，物体が放射をより 吸収しやすい場合には，その物体は，その波長と温度で，より強い熱放射現象を示します。黒体が，理想的な表面の性質を持つ場合には，全波 長の放射を完全に吸収します。よってそれは，所定の温度での，最大量の熱放射を行います。熱放射の温度依存性を調べる場合，このような物体 が仮定されます。

黒体放射S の温度依存性は，シュテファン＝ボルツマンの法則によって表されます。

(1)

ここで，T は絶対温度で表示した，物体の温度を表します。
また，は，シュテファン＝ボルツマン定数を表します。

物体は，熱放射と同時に，周囲からの放射を吸収するので，放射強度を直接測定することはできません。そこで，放射強度の測定値を，以下のように変更する必要があります。

(2)

ここで，Toは絶対温度で表示した，周囲の環境の温度を表します。白熱電球が発する光も，熱放射の一種です。この場合には，フィラメン トが発する熱のかなりの部分が，可視光域の光に変わると仮定することにより，フィラメントの温度が求められます。ここでは，全放射強度が，黒 体放射と同じ温度依存性を持つことと，フィラメントが全周波数の放射を，εの割合で吸収することを仮定します

(3)

本実験では，放射強度の温度依存性を求めるために，このような放射熱の吸収特性を持つ物質である，タングステンのフィラメントを備えた白熱電球を使用します。相対的な電磁波強度を計測する目的で，モル型熱電対列を使用します。フィラメントの温度は，その抵抗値の温度依存性を利用して求めることができます：

(4)

ここで，Roは，環境温度Toにおける抵抗値を表します。また，係数αは，タングステンに対して，という値になります。

抵抗値Rは，4線式熱電対を使用することにより，非常に正確に測定できます。

評価

以下の式が，式(4)から導出できます。

ただし（4）式は，単に良い近似であるというに過ぎません。より正確な結果を得るには，ステファン・ボルツマン電球の取扱説明書に掲載された表を使用することができます。

本実験では，温度をかなり高く設定することにより，式（3）の環境温度を無視することが可能です。これにより，放射熱の絶対強度の代わりに，熱電対の起電力を読み取って，これを相対強度の指標に使う事が可能です。この場合には，式（3）は次のように書き換えられます。

これは，In（Uth）対In（T）のグラフを描くと，全測定値が，傾き4の直線上に載ることを意味します。

参考資料