万有引力定数

実験番号:UE1010300
キャベンディッシュのねじり秤は,精密測定が可能なねじり秤と,それに取り付けられた2個の小鉛球を,主要な構成要素としています。さらに,2個の大きな鉛球が,これらの小鉛球に引力の効果を及ぼすように,小鉛球の傍に設置されます。これにより,ねじり秤の平衡位置が,2個の大きな鉛球によって決められることになります。
2個の大球を,小球に関して最初の位置と対称的な,第2の位置に移動させると,ねじり秤は,短時間の振動の後に,新しい平衡位置に落ち着きます。最初の位置と第2の位置での小球の位置を測定することにより,万有引力定数の決定が可能になります。重力とねじり秤の復元トルクとの間のつり合いが,この測定を決定する因子になります。
ノイズと信号中の不要な振動因子が大幅に低減された差分容量センサーを使って,ねじり秤の振動を計測することによって,測定を実行します。ねじり秤を吊り下げるタングステンワイヤーは,非常に細く作られているので,振動周期は二,三分程度になっています。これにより,一時間の実験中に,平衡位置を中心とする,数回の振動の観察が可能です。
実験に必要な機器
- U40205:万有引力測定用キャベンディッシュのねじり秤 ×1
- U22000:レーザーダイオード・赤・650nm ×1
- U13265:支柱用台座 ×1
- U13255:角型ムッフ ×1
- U15000:ステンレス鋼製支柱・10cm ×1
別途必要な機器
- 電子はかり(5000g) x1
- Windows PC x1
- ノギス・150mm x1
実験解説書
基本原理
二つの物体間に働く重力を実験室内で測定する際には,実験器具の周囲にあるあらゆる物体の質量が,測定結果に影響を与えることは避けられません。ところが,キャベンディッシュのねじり秤は,質量を持つ球体を,対称位置に配置することにより,この問題を回避しています。
キャベンディッシュのねじり秤は,精密測定が可能なねじり秤と,それに取り付けられた2個の小鉛球を,主要な構成要素としています。さらに,2個の大きな鉛球が,これらの小鉛球に引力の効果を及ぼすように,小鉛球の傍に設置されます。これにより,ねじり秤の平衡位置が,2個の大きな鉛球によって決められることになります。2個の大球を,小球に関して最初の位置と対称的な,第2の位置に移動させると,ねじり秤は,短時間の振動の後に,新しい平衡位置に落ち着きます。最初の位置と第2の位置での小球の位置を測定することにより,万有引力定数の決定が可能になります。重力とねじり秤の復元トルクとの間のつり合いが,この測定を決定する因子になります。
重力は,次の式で与えられます:
(1)![]()
- G :万有引力定数
- m1 :小鉛球の質量
- m2 :大鉛球の質量
- d :測定時における,小鉛球と大鉛球間の距離
計測時に大鉛球を設置すると,ねじり秤は平衡位置からずらされます。
このずらす力によるトルクは,
(2)![]()
という式で表されます。ここで,距離r は,r:支持板の支点から小鉛球までの距離です。
ねじり秤が平衡位置から,角度φだけずらされると,
(3)![]()
で表される復元トルクが働きます。ここで,Dは,タングステンワイヤーの捩れ係数を表します。
この復元トルクは,ねじり秤の支持板を吊り下げている,タングステンワイヤーの捻れによるものです。平衡位置では,M1とM2は同じ値になります。
捩れ係数D は,平衡位置を中心とするねじり秤の振動周期T から,以下の式で求められます。
(4)![]()
慣性モーメントJ は,2個の小球の慣性モーメントJ1 と,支持板の慣性モーメントJk との和になります。
(5)![]()
2個の大鉛球に対して,測定が実行できる,2つの対称位置があります。これらの位置における,平衡位置からのずれの角度を,φとφ’ とします。これらの角度に対応する,ずれのトルクは,大きさが同じで互いに逆向きになります。 したがって,平衡状態においては,(2)式と(3)式から,以下の式が得られます。
(6)![]()
実験で,ねじり秤の振動は,ノイズと信号中の不要な振動因子が大幅に低減される,差分容量センサーを使って計測します。ねじり秤を吊り下げるタングステンワイヤーは,非常に細く作られているので,振動周期は二,三分程度になっています。これにより,一時間の実験中に,平衡位置を中心とする,数回の振動の観察が可能です。ねじり秤に取り付けられた鏡を使って,光を反射させることにより,捩れ振動を裸眼で追うことが可能です。これにより,ねじり秤の必要な調整と校正が非常に容易になります。
評価
式(1),(4),(5),(6)を組み合わせることにより,以下の式が得られます。![]()
この式は,2個の小球が,より離れた側の大球による引力も受けていることを考慮していないので,この式によるねじり秤のトルクの計算値は,過去の類似の計算値に比べて,少々小さな値になります。
参考資料
-
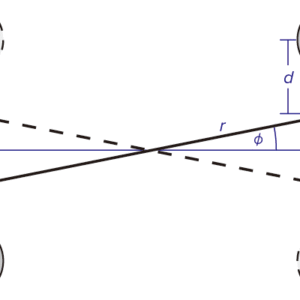
図1:キャベンディッシュのねじり秤による測定装置の模式図
-
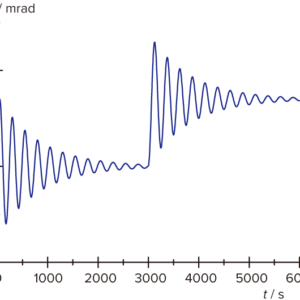
図2:2個の大鉛球の位置を二度変更した場合の,ねじり秤のずれの角 度の時間変動