斜方投射

実験番号:UE1030400
物体(ここではプラスチック球)を重力が働いている中で斜方投射すると,軌跡は放物線と呼ばれる初速度と投げ上げる角度に依存した軌跡を描きます。この曲線を測定します。
実験の手順
- 斜方投射した物体の到達距離を,初速度と角度の関数として測定します。
- 最大到達距離から初速度を計算します。
- 放物線をグラフにプロットします。
- 水平方向速度と垂直方向速度が独立であることを確認します。
実験に必要な機器
- U10360 放物投射装置 ×1
- U10361 放物投射装置固定具 ×1
- U8401560 垂直定規・1m ×1
- U8401570 定規用カーソルセット ×1
- U8611200 万能クランプ式台座 ×1
- 巻尺・2m ×1
実験解説書
基本原理
速度は運動方程式より,x,y,z方向それぞれ独立であるので,重力下で斜方投射した場合は,水平方向に一定速度で進み,垂直方向は重力下での鉛直投げ上げの場合と一致します。この為放物線は,投げ上げる角度αと初速度v0に依存します。理論的に放物線を計算する場合,簡単にするためにプラスチック球の中心に質点を取り,空気抵抗や球の回転を無視します。そして初期状態では,質点が座標原点に位置しています。
水平方向には速度一定で下記のようになります。
(1)![]()
一定速度で進むのでt 秒後のx 座標は
(2)![]() となります。
となります。
垂直方向では重力の影響下にあるので,次のように書けます。
(3)![]()
その為t 秒後のy 座標は
(4)![]() です。
です。
この式からtを消し,xとの関係に直すと放物線の式が出ます。
(5)![]()
vy=0 で高度が最大になるので,その時間t1 は次のように表せます。
(6)![]()
落下するまでの時間t2 は,高度最大になる時間の2 倍であるので
(7)![]()
となります。(y(t) の式でy=0としても求まります。)
時間が分かったので,最高高度hと到達距離s はそれぞれ
(8)![]()
(9)![]()
と求まります。
実験では垂直定規とカーソルを使い,角度と初速度に対する高度を調べていきます。
最大到達距離smax は,投射角45°の時になります。ここから逆算し初速度v0 は
(10)![]() と計算できます。
と計算できます。
実験では空気抵抗は無視できず,実験データと理論値とは若干のズレが出ます。
参考資料
-
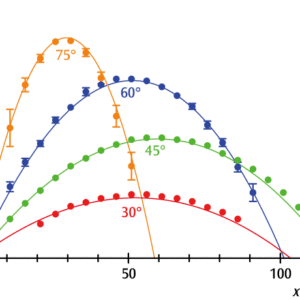
図1: 最小発射速度での様々な角度に対する軌道の,実測値と計算値(計算値は空気抵抗を考慮しています)