振り子の周期

実験番号:UE1050201
振動面を垂直から傾けていくことで,実際に振動に寄与する重力成分が小さくなり,振動の周期T が長くなります。
実験の手順
- 実際に働く重力の有効成分を変化させて,振動の周期T を測定します。
- 棒振り子の長さLを変化させて,振動の周期T を測定します。
実験に必要な機器
- U8403950:重力加速度可変振り子 ×1
- U13270:水平調整式三脚・支持穴2つ付き・15cm ×1
- U15002:ステンレス鋼製支柱・47cm ×1
- ストップウォッチ(別途ご用意ください)
実験解説書
基本原理
振り子の周期T は,振り子の長さL と重力加速度g で計算できます。振動面を垂直から傾けていくことにより,重力加速度の有効成分を変化(減少)させることができます。
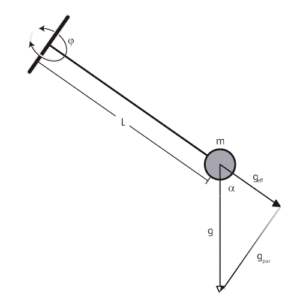
振動面が傾いていくと,振り子と垂直に働く重力加速度成分g Parは振動に寄与しません(図1 参照)。残りの振り子と平行な重力加速度成分g eff だけが振動に寄与し,振動面の傾きをαとするとg effは次のように表せます。
(1)![]()
この状態で振り子を平衡点から角度だけ動かすと,平衡点に向かって復元力F が働きます。 (振り子は振動面内に固定されているため通常の振り子と同じです。)
(2)![]()
角度φが小さいとすると,運動方程式は
(3)![]()
となります。
これより角振動数ω は次のようになります。
(4)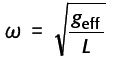
周期T はωより
(5 )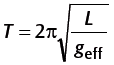
となります。
振動面の傾きを大きくするほどg effは小さくなるので周期T は長くなります。
参考資料
-
図1:重力加速度可変振り子概念図
-
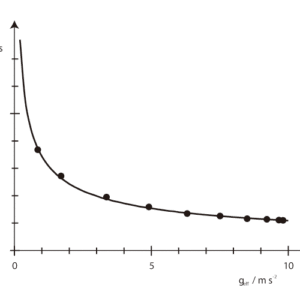
図2:有効重力成分に対する振り子の周期,理論値曲線は振り子の長さ L=30cmで計算