平らな梁(はり)のたわみ

実験番号:UE1090200
水平に保持された平らな梁の外力によるたわみ変形への抗力は,変形量が梁の長さよりはるかに小さい場合,数学的に計算することができます。この場合,梁の変形は梁を構成する材料のヤング率 E に比例します。この実験では既知の力による梁の変形を測定し,その結果を使ってスチールとアルミニウムのヤング率を求めます。
実験の手順
- 梁(はり)の中心部分に負荷をかけた場合と,中心からズレた部分に負荷をかけた場合とで梁各点での変形を測定します。
- 梁に加える力を変えた場合の梁の変形を測定します。
- 梁の長さ・幅・厚みへの変形の依存性と,梁材料と変形の関係を測定し,各材料のヤング率を求めます。
実験に必要な機器
- U8557260 ヤング率測定実験器 ×1
- U8557270 ヤング率測定実験拡張セット ×1
- U10070 外側マイクロメーター ×1
- 巻尺・2m x1(別途ご用意ください)
実験解説書
基本原理
平らで水平に保たれた梁の外力によるたわみ変形への抗力は,変形の程度が梁の長さよりはるかに小さい場合,曲げモーメントを使って数学的に計算することができます。以下の計算から分かるように,変形は梁材料のヤング率 E に比例します。そのため,既知の力による梁の変形測定から材料のヤング率が求められます。
(計算詳細については別紙「Appendix:梁のたわみの計算」を参照してください。)
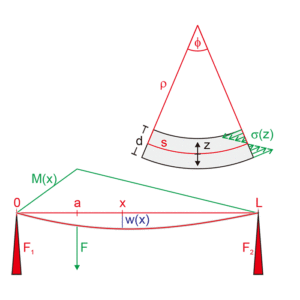
応力の計算をする際は,梁を部材軸に平行に薄切りしたセグメントに分割します。これらのセグメントは,梁のたわみにより,たわんだ内側で圧縮され,外側では引き延ばされます。よって,部材軸(=中央部分)に対して外側は引張,内側は圧縮されます。一方,部材軸部分のセグメントは圧縮や引張をしません。セグメントの引張や圧縮によるひずみεと圧縮や引張に伴う応力 σは,中央部分のセグメントからの距離 z に依存します。(図1)
(1) ε(z)=Δs(z)s(z)=zρ(z)
ρ(x): たわみによる局所的な曲率半径
また,フックの法則より
σ(z)=E⋅ε(z)
σ(x):応力,E:材料のヤング率
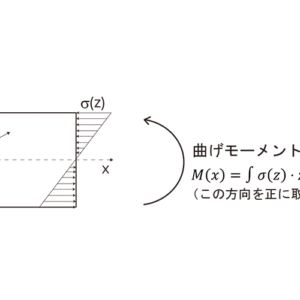
このたわみによる応力は部材軸に垂直な面を回転させようとする力のモーメント,曲げモーメントとして計算できます。(図2)
(2) M(x)=∫Aσ(z)⋅z⋅dA=E⋅Iρ(x)
ここでI=∫Az2⋅dAは,断面の慣性モーメントを表します。
この実験では曲率半径ρ(x) は直接測定せずに圧縮や引張をしない中央部分セグメントのz方向への変位 w(x) を測定します。セグメントの変形による変位w(x)の変化 dw(x)/dx が梁の長さLに比べ充分小さい場合には,w(x)とM(x)は次の式で結ばれます。
(3) d2w(x)dx2=1ρ(x)=M(x)E⋅I
これから,M(x)が決定されればw(x)は2階の微分方程式を解くことで求まります。
両端で支持され下向きの力 F が点aで作用している,長さ L の梁について調べます。平衡状態では,梁に作用する全ての力の総和はゼロになります。
(4)F1+F2–F=0
同様に,梁に作用するすべての力のモーメントの総和もゼロになります。
(5) F2⋅L–F⋅a=0
梁の両端では変位0かつ曲率0なので,M(0) = M(L) = 0 および w(0) = w(L) = 0 となります。これから M(x) が決定できます。
(6) M(ζ)={F⋅L⋅(1−α)⋅ζ:ζ≤αF⋅L⋅α⋅(1–ζ):ζ>α
ここで,0≤α=αL≤1,0≤ζ=xL≤1です。
よって変位w(x)は(3)より次のように求まります。
(7) w(ζ)={F⋅L3E⋅I⋅[(1−α6)⋅ζ3−(α36−α22+α3)⋅ζ]:ζ≤αF⋅L3E⋅I⋅[α36–(α36+α3)⋅ζ+α2⋅ζ2–α6⋅ζ3]:ζ>α
- 実験は次の手順で行います。
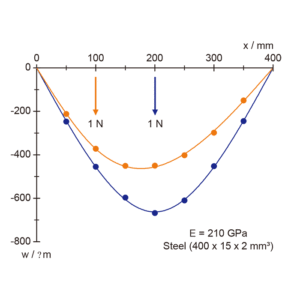
- 梁の中央 (ζ= 0.5) に負荷を加えた場合と,中央以外 (ζ< 0.5) に負荷を加えた場合とで計測し,計算との検証を行います。
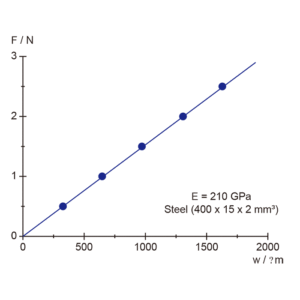
- フックの法則が成り立っていることを,梁の中央にかける負荷(力)を変えて変位最大値と負荷の大きさが比例していることを確かめます。
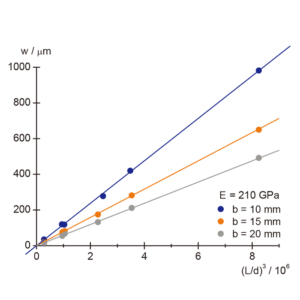
- 変位が(L/d)3に比例することを,様々な形状の梁を使って確認します。
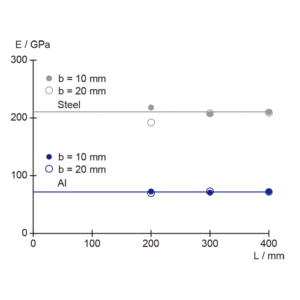
- 梁の変位と負荷からそれぞれのヤング率を計算し,文献値と比較・検証します。
評価
梁の中央に負荷を加えた場合には
(8) w(x=L2,α=L2)=−F⋅L348E⋅I
梁が幅 b ,厚さ dの場合,断面二次モーメントは以下のようになります。
I=∫Az2⋅dA=∫d2−d2z2⋅b⋅dz=d312⋅b
これから(8)は次のようになります。
w(x=L2,α=L2)=−F⋅L34E⋅d3⋅b
- 参考)ヤング率(理科年表から抜粋)
- 鉄(鋼)=20.1-21.6×1010 Pa
- アルミニウム=7.03×1010 Pa
参考資料
-
図1:梁のたわみと変形の概略図)
-
図2:曲げモーメントの図)
-
図3:梁の中央と中央以外に負荷を加えた場合の変位w(x)(測定値と計算値の比較))
-
図4:スチールでのフックの法則の検証(中央に負荷をかけたときの変位最大値と負荷の関係))
-
図5:w(x)と (L/d)3 の関係(負荷1Nを梁中央にかけた場合の変位最大値))
-
図6:スチールとアルミニウムのヤング率(測定値と文献値の比較))