円柱形ロッドのねじり変形

実験番号:UE1090300
固体を変形させるには力が必要です。加える力が大きすぎなければ,固体の変形と外力は比例します。(フックの法則)
本実験では一端を固定した円柱形の材料にねじりを加えますが,抗力はその材質・形状・力を印加する向きに依存します。フックの法則が成り立つ範囲であれば,力を取り除いた後は単振動します。力学的な解析から振動周期への材質のせん断弾性係数や形状(円柱の長さ・半径)への依存性を調べ,実験結果から検証します。
実験の手順
- 円柱形ロッドのねじり外力に対する比例係数と長さLの関係を測定します。
- ねじり外力とロッド半径の関係を測定します。
- 各ロッドのせん断弾性係数を求めます。
実験に必要な機器
実験解説書
基本原理
固体をねじったときの抗力は,力が大きすぎない範囲では,ねじった角度に比例するというフックの法則に従います。一端を固定し他端を自由にした円柱形ロッドでは外力を取り除いた後は復元力により単振動します。振動の力学的な解析から,単振動周期と材質のせん断弾性係数・ロッドの形状の関係を調べ,実験結果から検証します。
実験では付加錘を用い,慣性モーメントを変えて振動周期を2回測定することで,慣性モーメントを求めることなくせん断弾性係数を求めます。
円柱形ロッドの微小ねじり変形は,内部各断面が円形のまま不変という単純ねじり変形理論が適用できます。
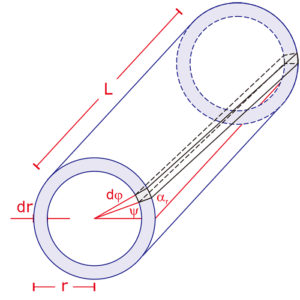
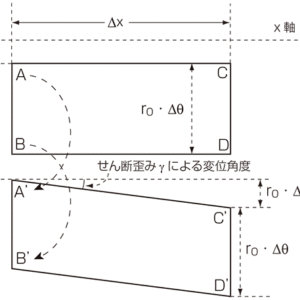
図1,2から分かるように固定端から軸(中心軸)に沿って距離xだけ離れた部分とx+Δxだけ離れた部分の側面は長方形から平行四辺形に変形します。この変形はせん断変形で,次式のようにせん断応力τとせん断歪みγの関係として表せます。
(1) \( \tau = G \cdot \gamma \)
ここでG:せん断弾性係数
せん断歪みγは次のように分解できます。
(2) \( \gamma = r_0 \cdot \frac {d \varphi} {d x} \)
r0:円柱形ロッドの半径
断面が変形しないことから明らかにロッド内部でのせん断歪みγiも中心からの距離rを使って,
(3) \( \gamma_i = r \cdot \frac {d \varphi} {dx} \)
と表せます。
(1),(2)式より,せん断歪みγiによるせん断応力τiが各断面内面積素に働く力のモーメントとなり,平面内のせん断応力全量Mは平面内の足し合わせ(積分)となります。
(4) \( M = \int_A \tau_i \cdot r \cdot dA = G \cdot \frac {d \varphi} {dx} \cdot \int^{r_0}_0 \int^{2 pi}_0 r^3 \cdot d \theta \cdot dr = \frac {\pi} {2} \cdot G \cdot \frac {d \varphi} {dx} \cdot r^4_0 \)
ここで \( \int_A r^2 \cdot dA = \int^{2 \pi}_0 \int^{r_0}_0 r^3 \cdot dr \cdot d \theta \)を断面二次極モーメントと呼びます。
Mは外力による力のモーメントと釣り合います。
また \( M = G \cdot J \cdot \frac {d \varphi} {dx} \)と表わしGJをねじり剛性と呼びます。\( \frac {d \varphi} {dx} \)はねじり率にあたりますが,この解析では一定値であり外力のモーメントが加わる自由端の角度をΨとすると
(5) \( \frac {d \varphi} {dx} = \frac { \Psi} {L} \) \( \therefore \, \, M = \frac { \pi \cdot G \cdot r_0^4} {2L} \cdot \Psi = D \cdot \Psi \)
Dは一定値なのでねじり角度とねじりモーメントが比例することが分かります。
(5)式から円柱形ロッドをねじるのに必要な力のモーメントは,
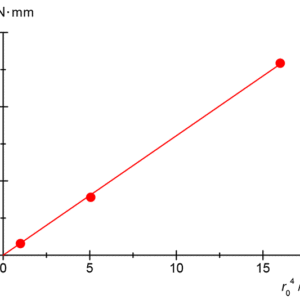
- ロッド半径の4乗に比例する事
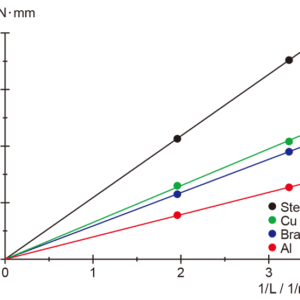
- ロッド長さLに反比例する事
- ロッドの材質に依存するせん断弾性係数Gに比例する事
が分かります。
サンプルの慣性モーメントをIとすると\( I \cdot \frac {d^2 \varphi} {dx^2} = M = D \cdot \Psi \)より,振動周期Tは次のようになります。
(6) \( T = 2 \pi \cdot \sqrt{ \frac {I} {D}} \)
本実験では回転ディスクを付けた状態での慣性モーメントは求めず,付加錘を付けた状態と付けない状態の2種でそれぞれ周期を測定することで比例定数Dを計算します。
付加錘は互いに180°位置に置かれます。錘は円柱形なので中心からの質量分布が対称となっています。その為,質量が中心(重心)に集中しているとしてサンプル全体の慣性モーメントを計算しても十分な精度を持ちます。(確認計算)
この時の慣性モーメントI1は,サンプル下部(自由端側)に付いている回転ディスクの半径をRとすれば,
(7) \( I_1 = I_0 + 2m \cdot R^2 \)
となります。
評価
(7)式より付加錘の有無で振動周期Tは次のようになります。
\( T_0 = 2 \pi \cdot \sqrt { \frac {I_0} {D}} \), \( T_1 = 2 \pi \cdot \sqrt { \frac {I_1} {D}} = 2 \pi \cdot \sqrt { \frac {I_0 + 2m \cdot R^2} {D}} \)
よって上二式からI0を消せば,
\( D = 4 \pi^2 \cdot \frac {2m \cdot R^2} {T_1^2 – T_0^2} \)
と計算できる事が分かります。
参考資料
-
図1:円柱形ロッドのねじり変形図
-
図2:図1の円柱形ロッド側面のねじりによる変形詳細
-
図3:(5)式の比例係数Dとr04のグラフ(アルミニウムL=500mm)
-
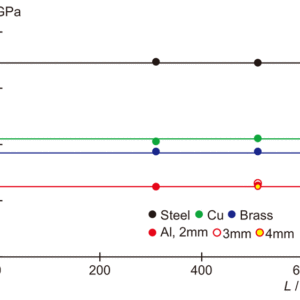
図4:Dと1/Lのグラフ
-
図5:せん断弾性係数G(測定値と文献値の比較)