定在波

実験番号:UE1050700
力学的波動の定在波を観察します。縦波はコイルばねの振動で,横波は水平に張った紐を使います。定在波は自由端でも存在できますが,本実験では固定端での定在波を扱います。縦波のばねも横波の紐も片側は固定端となっていて,反対は振動発生器に接続されます。こちら側を良い近似で固定端として扱えます。この扱いで定在波の振動数と節の数,波長と波動の伝播速度の関係を考察します。
実験の手順
- コイルばねで縦波,水平に渡した紐で横波のそれぞれ定在波を作ります。
- 定在波の節の数とその時の振動数(固有振動数)を測定します。
- その結果から波長λnと波動の伝播速度cを決定します。
実験に必要な機器
- U56003:縦波観察用バネ ×1
- U85560081:横波実験用ロープセット ×1
- U56001:振動発生装置 ×1
- U8533600-115:関数発生器 ×1
- U20034:高精度バネばかり・5N ×1
- U13812:プラグ付き安全リード線・75cm・2本セット ×1
- 巻尺・2m ×1(別途ご用意ください)
実験解説書
英語版 実験手順書 ダウンロード(参考,一部取り扱いのない製品も含まれています)
基本原理
定在波は振幅・振動数・波長の等しい逆方向に進む波の重ね合わせによって生じます。これは両側固定端,両側開放端,片側が固定端で反対が自由端,波の媒質が閉じた(閉曲線状)状態などで起こりえます。本実験では両側固定端で進行波と反射波という正弦波の重ね合わせによる定在波を縦波と横波の場合で観察・測定します。安定した正弦波の重ね合わせは正弦波である事,その時の振動数と波長の関係が媒質長で決まってくる事などが分かります。
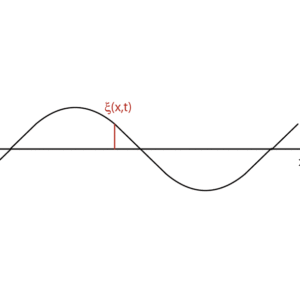
一次元の波動を考えます。この波が縦波でも横波でも以下の数学的取り扱いは成り立ちます。振幅ξ0で振動数f,波長λの正弦波の波源が原点x=0にあるとします。この時,任意の(x,t)での波は次の式で表せます。
(1)
ここでは初期位相を0としています。
2πはどちらの項にも付くことと,項は位相として表わす方が自然なので,次の2つの量で書き換えます。

(2)![]()
この波の進む向きは次のように分かります。
注目している位相がtからt+Δt に時間経過したとき(Δt>0),同じ位相はこの増加分を打ち消すように
(3)![]()
の位置に移動します。右辺の量は全て正なのでこの変位は座標の+方向,つまり波が左から右に進んでいることが分かります。
x>0(=L)に固定端があり,ここで反射された波は上の考察から次式になります。また,固定端での反射なので位相がπずれます。
(4)
実際に観測される波ξ は波源からの進行波と固定端からの反射波の重ね合わせとなります。
(5)
安定した定在波は固定端で振幅が0であることから,次の条件が出ます。
(6)
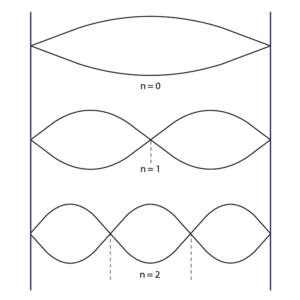
ここでnは0以上の整数を表わします。nは定在波の両端を除いた節の数に対応しています(図2)。また,この条件を満たす振動数を(その物質の)固有振動数と呼びます。
波動の伝播速度vは波の空間的な様子を考えると振動数f,波長λと次のように関係づけられます。
(7)![]()
(8)
本実験では固定端での定在波を扱います。縦波のばねも横波の紐も片側は固定端となっていて,反対は振動発生装置に接続されます。振動発生装置は小さな振幅の振動を起こしますので,こちら側を良い近似で固定端として扱えます。
評価
定在波の振動数(固有振動数)を節の数を横軸にグラフにすると各点は直線に載り,傾きは
(9)![]()
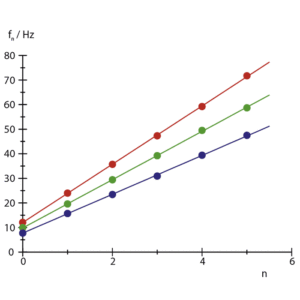
となります。その為,Lが既知であれば固有振動数fを測定することで波の伝播速度vが計算できます。 また,紐の横波の伝播速度は張力の平方根に比例することが知られています。その為,同じ波長(=n が等しい)の定在波でも張力を変えることで固有振動数fが変化します(図4)。
参考資料
-
図1:変位ξ(x,t)の図示
-
図2:節の数nと定在波
-
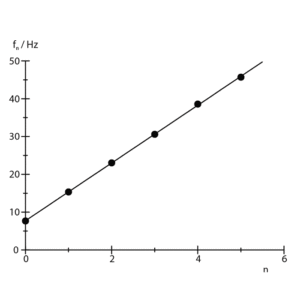
図3:コイルばねの縦波での節と固有振動数のグラフ
-
図4:紐の横波での節と固有振動数のグラフ(張力を3通りに変えています)