定在波からの音速の決定

音波は縦波として気体中を伝播します。群速度は位相速度と一致します。本実験では,両端が閉管のクント管内で定在波を発生させます。基本周波数をクント管の長さを変えて測定し,基音と倍音の周波数もクント管の長さを固定して測定します。
実験の手順
- 両端が閉管のクント管内で定在波を発生させます。
- 定在波の基本周波数を,クント管の長さの関数として測定します。
- 固定長のクント管に対する基本と倍音の周波数を測定します。
- 共振周波数から波の伝播速度を決定します。
実験に必要な機器
- U8498308:クント管・E型 ×1
- U8498282:プローブマイク・長軸型 ×1
- U8498283-115:マイクロホンボックス (100 V, 50/60 Hz) ×1
- U8533600-115:関数発生器 ×1
- U11830:USBオシロスコープ2x25MHz ×1
- U11257:BNC-4mmプラグ変換ケーブル ×1
- U13812:プラグ付き安全リード線・75cm・2本セット ×1
- Windows PC ×1
- *オシロの代わりにマルチメーターでも可
実験解説書
英語版 実験手順書 ダウンロード(参考,一部取り扱いのない製品も含まれています)
基本原理
適切な周波数の音波をクント管の一端からスピーカーで発生させ,閉管になった他端で反射させることにより,クント管内に定常波を生じます。クント管の長さが既知の場合には,共振周波数と高調波のノード数から,音波の伝播速度が測定できます。
空気や他の気体中の音波は,圧力と密度を急激に変化させることによって伝播します。この様子は,大気圧下にある気体に更に音圧を加える形で記述できます。音圧pの代わりに,音速vを使って音波を記述することも可能です。音響工学で言う粒子速度のことです。またこれは,振動する媒質中の時刻tでの任意の点xにおける,気体分子の平均速度を意味します。音波の圧力と速度は,たとえば,オイラーの運動方程式によって下記のように表せます。
(1)
クント管中で,音波は管の長さ方向に沿って伝播するので,(1)式と連続の式から,波動方程式が得られます。これは,音波の圧力と速度の双方に適用できます。
(2) または,
または,
本実験では,クント管の端部で反射される高調波について調べます。波動方程式の解を見つけるには,進行波と反射波の重ね合わせを考える必要があります。
(3)![]()

この場合,以下の関係式が成り立ちます。
(4)![]()
これらの解を式(1)に代入し,進行波と反射波を個別に考えることにより,以下の式が導かれます。
(5)
ここで使われた,
(6)![]()
という量は音響インピーダンスと呼ばれ,音波が媒質内を伝播する際に媒質自体から受ける抵抗に対応します。これは,音波が音響インピーダンス W の壁により反射される場合を考える際に,主要な役割を演じます。 これらに対して,以下の式があてはまります。
(7)
本実験では, W はZよりもはるかに大きいので,rv =-1 , rp =1 と仮定することが可能です。
以後の説明を簡単にするために反射壁が x=0 の位置にあるとすると,音波の空間成分は,式(3)から,以下のように導出できます。
(8) と,
と,
これらの項のうちで,実数成分のみが現実の物理現象に関係してきます。これらは,管の端部の壁の位置(x=0)で,音圧の振動の腹と音速の振動の節とを持つ定常波の音波に対応します。音速は音圧よりも,位相が90°だけ前方にシフトしています。
音波は,壁から距離Lだけ離れた位置にあるスピーカーを使って発生させます。この音波は,周波数 f で振動します。この位置においても,音圧は振動の腹になり,音速は振動の節になります。このような境界条件は,Lが音波の半波長の整数倍の場合にのみ設定できます。
(9)![]()
この場合,方程式(3)から共鳴を発生させるには,振動周波数が次の条件を満たしている必要があります。
(10)![]()
実験では,プローブマイクを使って,反射壁で音圧を測定しながらスピーカーから発生させる周波数 f を連続的に変化させます。こうすると,プローブマイクからの信号が最大振幅になるときに,共振現象が発生します。
評価
方程式(10)から定まる共振周波数 fn に対して,波長は以下の式で与えられます。

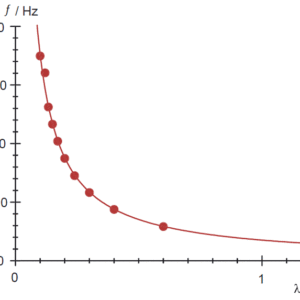
式(3)を確かめて,波長を測定するには,周波数 f と波長 λ の関係をグラフにプロットします。
参考資料
-
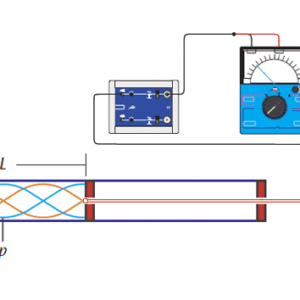
図1:実験装置の構成の概略図
-
図2:周波数と波長の関係を表すグラフ