反射の法則

実験番号:UE4010000
光が反射するときは入射角と反射角が等しくなります。これを反射の法則といい,入射面が平面ばかりでなく曲面でも成り立ちます。曲面の場合は光が当たる点の接平面に対し反射の法則が成り立つので,単純な凹面や凸面では曲率が小さいと焦点を反射光が焦点を結びます。 反対に曲率が小さいと見なせない場合,焦点はできません。
実験の手順
- 平面鏡を使って反射の法則を確かめます。
- 凹面鏡で光を反射させ焦点距離を測定し,反射の法則を確かめます。
- 凸面鏡を使って焦点距離を測定します。
実験に必要な機器
- U10300:光学台,1000mm・D型×1
- U103101 キャリア・D型・幅5cm,軸さや高6cm×4
- U21882:集光レンズ付き光学実験用LEDランプ×1
- 絞り×1
- U8474000:遮蔽板付き光学部品ホルダー×1
- 幾何光学学習セット・角度計付き×1
- U17040:光学用スリットセット×1
実験解説書
基本原理
光が反射するときは入射角と反射角が等しくなります。このため平行に入射した複数の光線は,平面での反射後も平行のままです。一方,凹面鏡のような曲面に入射した複数の光線は反射後,平行光線とはなりません。その代り凹面の曲率が小さい場合は,焦点で光線が交わります。この場合でも反射の法則は成り立っています。
反射の問題に集中するため,以下全てのケースで理想的な鏡に単色光が入射した場合を考えます。 光がある面に入射する角度をαとすると,反射された光がその面となす角度βはαと等しくなります。
(1)\(\alpha =\beta\)
これを反射の法則といいます。
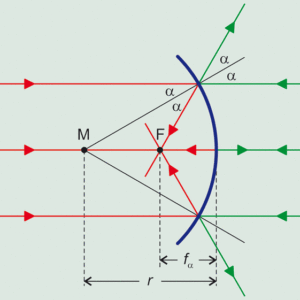
平行光線が凹面鏡に入射した場合も反射の法則が成り立ち,入射光の当たる点それぞれの接平面でα=βとなる反射光が観察されます。その為,もし入射平行光が凹面鏡の光軸に平行であれば反射光は,反射光は凹面鏡底部から次の距離fαの点で交わります。(図1参照)
(2)\(f_{ \alpha }=r-\bar { MF } =r\cdot \left( 1-\frac { 1 }{ 2\cos { \alpha } } \right)\)
今,凹面鏡の曲率が小さくcosα~1と見なせるならば上式は,αに無関係に,次のようになります。
(3)\( f=\frac { r }{ 2 } \)
cosα~1という条件は,r>>1 または入射平行光が凹面鏡光軸と非常に近いということです。この条件が成り立つと見なせる範囲で,曲率一定の凹面鏡の光軸に平行に入射した光の反射は,光源の距離に関係なく全て一点(焦点)で交わります。
上と同様の考え方で凸面鏡(曲率一定でr≫1)の焦点位置は負で次の式を満たします。
(4) \( f=-\frac { r }{ 2 } \)
本実験は次のように行います
- 光学台に各部品をセットして光軸中心を合わせます。(光源側に絞り,鏡側に3本スリットスライドをセットします。)
- 最初は平面鏡をセットし,反射の法則が成り立つことを平面鏡の角度を変えながら確かめます。
- 凹面鏡をセットし入射光が一点で交わることを確認します。この時の焦点距離fαを測定します。
- 次に凹面鏡の角度を変えたときの反射光を観察します。
- 凸面鏡を光軸に垂直にセットし,反射光から焦点距離を測定します。反射光を凸面鏡反対側に伸ばした時に交わる点です。
評価
凹面鏡を例に取りcosα~1と見なせない場合を考えます。この時,(1)式から入射した光の反射光は一点で交わりません。凹面が半径一定の単純な球面ではなく放物線(y=a⋅x2)の凹面では,平行光はどのように反射されるか,方眼紙に作図して検討してみましょう。
(y=a⋅x2の凹面ならば,y=1/4aの点で全ての反射光が交わるはずです。)
参考資料
-
図1:凹面鏡の反射光(赤)と凸面鏡の反射光(緑)の図示
-
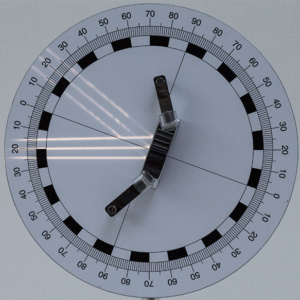
図2:平面鏡での平行光の反射
-
図3:凹面鏡での反射
-
図4:凸面鏡での反射