屈折の法則

実験番号：UE4010020

光の屈折率は媒質中の光速の比となります。その為，相対屈折率は入射の角度によらず一定です。屈折率が媒質の光速に依存することから臨界角度がある場合があり，それを超える入射角度では屈折は起こらず全反射します。

実験の手順

半円アクリル体を使って種々の角度で反射と屈折の法則を確認します。
媒質の順番が逆になると屈折率が逆数になることを確かめます。
臨界角度と屈折率の関係を調べ，全反射の現象を確かめます。

実験に必要な機器

お見積りフォーム

実験解説書

実験解説書ダウンロード（PDF）

基本原理

光の屈折も光が波である事からホイヘンスの原理を用いることで導けます。ここから絶対屈折率（真空に対する屈折率）がその媒質中での光速に依存することが分かります。相対屈折率（媒質1から媒質2へ光が入射するときの屈折率）は，それぞれの媒質中の光速の比として表わされます。

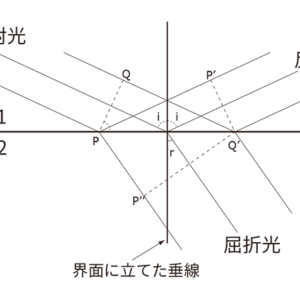
以下，全てのケースで入射光は単色光とします。光の波長による分散を考えないということです。光の屈折と反射は光が波である事からホイヘンスの原理を使って導けます。図1のように媒質1と媒質2の平坦な界面に光が入射する時を考えます。図1のそれぞれの方向に反射光・屈折光が進むならば，次のことが言えます。

反射の法則

P点で反射された光がP’点に到達したときにQ点の光がQ’点に到達します。P-Q’間の各点で反射した光は同時にP’-Q’線上に到達します（同一媒質中での光速は同一であることから）。P’-Q’線に垂直に反射光は進みます。ここから△PQQ’と△Q’P’Pは合同であり，界面に立てた垂線に入射光・反射光がそれぞれなす角は等しくなります。

屈折の法則

P点で屈折した光がP’’点に到達したときにQ点の光がQ’点に到達します。各媒質での光速をそれぞれc1，c2とすると次の関係を満たします。

\( \frac {PP”} {c_2}=\frac {QQ’} {c_1} \)

\( \frac {QQ’} {PP”}=\frac {c_1} {c_2} \)

\( \frac { \frac {QQ’} {PQ’}} { \frac {PP”} {PQ’}}=\frac {c_1} {c_2} \)

\( \therefore \frac { \sin { i } } {\sin { r } } =\frac {c_1} {c_2} =n_{12} \)

相対屈折率はn12それぞれの媒質中の光速比となり，入射角度が変わっても屈折率は一定となります。

相対屈折率という言葉は(1)式から明らかなように界面を構成する2つの媒質が決まった後，それぞれの光速から計算されます。相対屈折率は光速の比なので，ここから臨界角という概念が生まれます。媒質2での光速c2は決まっていますので，入射角が次の角度icを超えるとc2を越えるため屈折は起こらず，入射光は全て反射されます（全反射）。

\( \sin {i_c } = n_{12} \)

臨界角の条件は相対屈折率の値そのものなので，相対屈折率の値によっては全反射が起こらない界面も存在します。（例：空気→水では全反射は起こりません）

また絶対屈折率は真空に対する屈折率を言います。各媒質の絶対屈折率を使って相対屈折率を表わすこともできます。

\( \sin {i_c } = n_{1} \)

\( \therefore n_{12} = \frac {c_1 } {c_2 } = \frac {n_2 } {n_1 } \)

本実験は次のように行います

水平な台かホワイトボード上に半円アクリル体（大）を角度板（番号F）の角度が読みやすいように設置します。5光線レーザーは光線が1本になるよう設定し，半円体の中心に当たるように設置します。
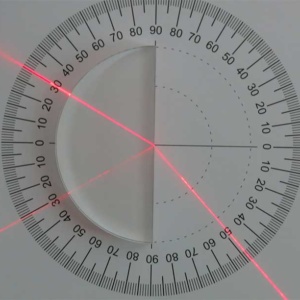
最初は半円体の水平面に光線が当たるようにし，反射角と屈折角を様々な入射角で測定します。（このセットのアクリル屈折率は，赤色レーザーで空気→アクリルの時に約1.46です。）
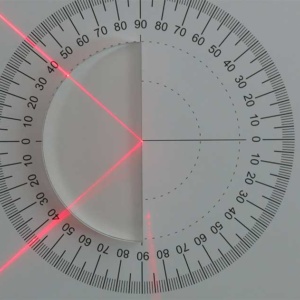
半円体の円弧に垂直に光線が当たるようにしてアクリル→空気での屈折角を様々な入射角で測定します。この時の屈折率が空気→アクリルでの屈折率の逆数になっていることを確かめます。
アクリル→空気での屈折の臨界角を測定します。臨界角icが\( \sin { i_{ c } } =\frac { 1 }{n_{空気\rightarrow アクリル} } \)になっていることを確かめます。
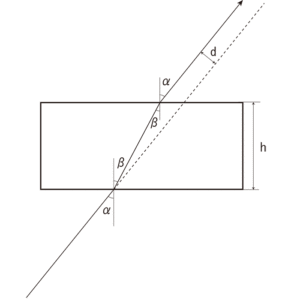
長方形アクリル体を設置します。光線がアクリル体を通過するときのズレ（図4）が次の式になることを様々な角度で検証します。
\( d= h \cdot \frac {\sin { (\alpha -\beta )} } { \cos { \beta } } \)
この状態で長方形アクリル体から出た光線に垂直に鏡を立てると，鏡による反射光が元の光線と同じ軌道をたどること（複数の光線が現れないこと）を確認します。これを光線逆行の原理と言います。
導波管（細長いアクリル体）を使い，全反射を観察します。
長方形アクリル体で3光線（狭）を当て，屈折が起きても平行光線は平行光線のままである事を確認します。
正三角形アクリル体に3光線を当てると，光線の順序が入れ替わること・二度内部で反射させると光線の上下が反転する事を検証します。

評価

長方形アクリル体での光線のズレdは角度βが屈折率で決まるので，入射角αと屈折率n（空気→アクリル）を用いて，次の式に帰着します。\( d= h \cdot \left( \sin { \alpha } -\cos { \alpha } \cdot \tan {\beta } \right) =h \cdot \sin { \alpha } \cdot \left( 1- \frac { \cos { \alpha } } { \sqrt {n^2 – \sin ^{ 2 }{ \alpha } } } \right) \)