単スリットの回折

実験番号:UE4030100
光の回折はホイヘンスの原理によって,スリットを通過した後のコヒーレントな素元波による波の重ね合わせで理解できます。スリット幅とスクリーンまでの距離が既知であれば,干渉縞の間隔を測定することで,波長を計算できます。
実験の手順
- スリット幅を変えて干渉縞を観察します。
- 波長の異なる光源で,スリット幅を変えて干渉縞を観察します。
- 細いワイヤーを用意し,これによる干渉縞と同一幅の単スリットによる干渉縞を比較します。(バビネの原理)
実験に必要な機器
- U8475240:光学台・1000mm・K型 ×1
- U8475350:光学キャリア・K型 ×2
- U8476675:可変スリット・K型 ×1
- U8475550:レーザー光源固定板・K型 ×1
- U22000:レーザーダイオード・赤・650nm ×1
- U22001:レーザーダイオード・緑・532nm ×1
- 細いワイヤー 適量(別途ご用意ください)
実験解説書
基本原理
スリットを通過した後の光は,スリット面のコヒーレントな素元波の重ね合わせで理解できます(ホイヘンスの原理)。各素元波の重ね合わせによる波面が,広がっていく光を記述します。また干渉も各素元波のスクリーンまでの距離に依存した位相差によって明暗のパターン(干渉縞)が記述できます。
光による干渉縞は,コヒーレントな光の光路差に依存する位相差で説明できます。つまり暗くなる(完全に打ち消し合う)部分では1/2波長の奇数倍位相がズレていて,明るい(強めあう)部分での位相差は波長の整数倍(0含む)となっています。
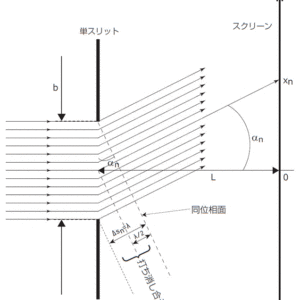
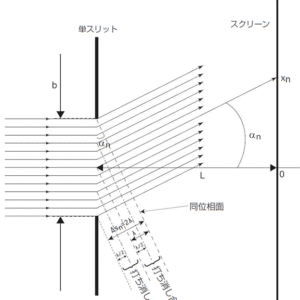
単スリットの場合もスリット面上で位相が揃っていますので,その面上の素元波の重ね合わせを考えます。干渉縞の暗部は次のように理解できます。単スリット中心からある角度αズレた位置のスクリーンに,同時に到達する素元波の波面は図の線で結んだものになり,各素元波の位相はズレています。図1スリット上下端での光路差が波長λだとするとスリットを仮想的に中心で縦半分に区切ると上半分と下半分で位相がλ/2ズレていることになり,打ち消し合ってスクリーン上の対応点は暗くなります。
上下で2λズレている場合(図2)は,縦に四つに区切ると上半分・下半分がそれぞれの1/4部分でλ/2ズレているので打ち消し合い,結果スクリーン上の対応点は暗くなります。3λ,4λについても区切りを増やして考えると同様に各区分が打ち消し合います。
まとめると,暗部(完全に打ち消し合う点)では光路差は下の条件を満たしています。
(1)\( \Delta s_{ n }=b\cdot sin \alpha _{ n }=n\cdot \lambda \)
ここでn=±1,±2,・・・の整数であり,bはスリット幅,αnはスリット中心からの角度となります(図1,2参照)。
干渉縞を観察すると強い光(0次,透過光)を中心として両側に対称に干渉縞が現れます。それゆえ干渉縞の位置を0次光の中心からの距離xで表わすと,スリット中心との角度αとの間に次の関係があります。
(2)\( x_{ n }=L\cdot tan \, \alpha _{ n }\)
L:スリットとスクリーンとの距離
Lがxより十分に大きければ,次のように近似できます。
\( \frac { x_{ n } }{ L } =tan \, \alpha _{ n }\sim \alpha _{ n }~,~n\cdot \frac { \lambda }{ b } =sin \, \alpha _{ n }\sim \,\alpha _{ n } \)
(3)\( \therefore x_{ n }=n\cdot \frac { \lambda \cdot L }{ b } =\Delta \cdot n \) ここで \(\Delta =\frac { \lambda \cdot L }{ b } \)
バビネの原理
スリットとそのネガ像は相補的な関係にあります。バビネの原理によれば,回折の影響を受けない光が当たる部分を除くと,両者で同じ干渉縞が観察されます。それゆえ,両者の干渉縞の間隔は同一となります。
本実験では下記のように進めます。
- 赤色レーザー光源で様々なスリット幅で,単スリットの回折を観察します。
- 1.と同じ各スリット幅で,光源を緑色レーザーに変えて回折を観察します。
- 単スリット幅と同じ径の細いワイヤーによる回折を観察します。
評価
(3)式よりΔは横軸n縦軸xnのグラフの傾きとして求められます。また波長λは横軸1/b,縦軸Δ/Lの傾きとして与えられます。バビネの原理から毛髪による回折パターンを測定することで,太さ を推定するのも興味深い実験となります。
参考資料
-
図1:単スリットによる回折での位相差(光路差)
-
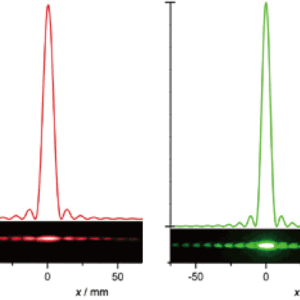
図2:計算回折強度と観測結果(b=0.3mm,L=4.62m)λ=650nm(赤)と532nm(緑)
-
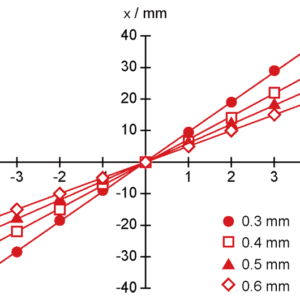
図3:各スリット幅での暗線位置と回折次数(λ=650nm,L=4.62m)
-
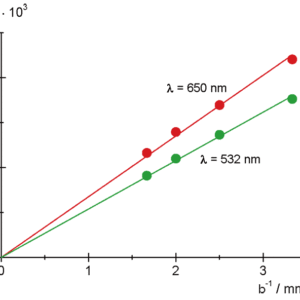
図4:スリット幅bの逆数でΔ/Lをプロット(グラフの傾きが波長λを与えます)
-
図1-補足:位相差が2λのとき