マリュスの法則

実験番号:UE4040100
マリュスの法則は,初期強度がI0 の直線偏光が検光子を通過した後,その強度が検光子の回転角φを用いて記述される事を示しています。この実験では光の強度は光センサーで測定します。
実験の手順
- 2枚の偏光板(偏光子,検光子)を通った光の強度を,検光子の回転角度φの関数として測定します。
- その結果からマリュスの法則を確認します。
実験に必要な機器
- U10302:光学台,500mm・D型 ×1
- U103111 キャリア・D型・幅5cm・軸さや高9cm ×4
- U21882:集光レンズ付き光学実験用LEDランプ ×1
- U22017:偏光フィルター ×2
- UCMA-BT50I:照度センサー,3レンジ ×1
- 1022269:照度センサー用ホルダー ×1
- UCMA-BTSC1:センサー接続ケーブル ×1
- 1022284:WiLab ×1
- Windows PC ×1(別途ご用意ください)
実験解説書
英語版 実験手順書 ダウンロード(参考,一部取り扱いのない製品も含まれています)
基本原理
光が横波である事はマクスウェル方程式から導かれます。横波,電場が光(電磁波)の進行方向に垂直である事から偏光という現象が存在します。端的な例は本実験のように偏光板を通過した後の光です。この時,磁場も電磁波の進行方向と垂直で,かつ,電場とも垂直である事がマクスウェル方程式から言えます。このため電場のみに注目し,ここでは電場の方向を偏光方向,電場と進行方向を含む面を偏光面と呼びます。
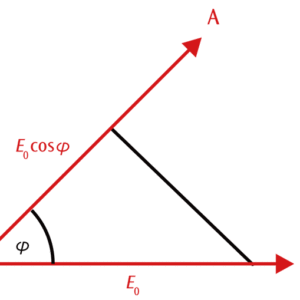
本実験では,光は2つの偏光板を通過します。最初に通る偏光板を偏光子,その後の偏光板を検光子と呼びます。偏光子と検光子の偏光軸が角度φをなしているとします。偏光子は1方向の偏光しか通しません。1方向の変更を直線偏光と呼びます。偏光子を通過した後の電場の振幅をE0とするとします。 検光子を通過した後の光の電場振幅は次式で与えられます。(図2参照)
(1)![]()
ここでφは偏光子と検光子の偏光軸の互いになす角度です。
実験では電場振幅ではなく,光の強度を測定します。光強度は電場振幅の二乗に比例します。これは電磁波が運ぶエネルギーはポインティング・ベクトルで表わされる事と,観測される光強度は振動数が大きいため電磁波強度の時間平均となるからです。
ポインティング・ベクトルSは次式で表わされます。
(2)![]()
真空では(物質中でなければ)![]() であり電場と磁場は直交していることから,光強度(大きさ)は
であり電場と磁場は直交していることから,光強度(大きさ)は![]() を一周期にわたり平均することで求まります。 単純な平面波を考えれば振動部分の一周期での平均は定数になるため,光強度は電場振幅E0の二乗に比例する事が分かります。
を一周期にわたり平均することで求まります。 単純な平面波を考えれば振動部分の一周期での平均は定数になるため,光強度は電場振幅E0の二乗に比例する事が分かります。
その為,検光子通過後の光強度は偏光子通過後の光強度を![]() と書き直すと次のようになります。
と書き直すと次のようになります。
(3)![]()
この式がマリュスの法則です。この式は検光子通過後の光強度を光センサーで測定することで検証できます。また![]() での光強度は検光子通過後の光ではなく,周囲の灯りからの光強度になります。この値を全測定値から差し引くことで,真の検光子通過後の光強度が求まります。
での光強度は検光子通過後の光ではなく,周囲の灯りからの光強度になります。この値を全測定値から差し引くことで,真の検光子通過後の光強度が求まります。
上記はジョーンズベクトルを使った計算でも示せます。ジョーンズベクトルは偏光した光の電場をx方向に振動する直線偏光と,y方向に振動する直線偏光の重ね合わせとして表現する計算手法です。そのため完全偏光の場合しか扱えません。
検光子の偏光軸をx軸に取ると偏光子を通過した直線偏光は角度-φ傾いています(基準を偏光子から検光子に変えたのでマイナスが付きます)。この時,ジョーンズベクトルは次の2成分のベクトルで表わされます。
(4)
検光子はこの場合x方向成分だけを通す働きをするので,検光子通過後のジョーンズベクトルは
(5)
となります。
(2)の計算の通り,光強度は電場振幅の二乗に比例するので(3)式が再び得られます。
評価
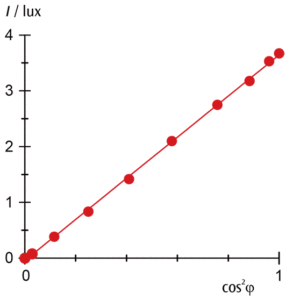
真の検光子通過後の光強度と検光子の角度度φをグラフにすると,その曲線の角度依存性が(3)式と一致する事が分かります。これをはっきりと見るために縦軸に光強度,横軸にcos2φを取ると,光強度Iが一直線に載ることが分かります。
参考資料
-
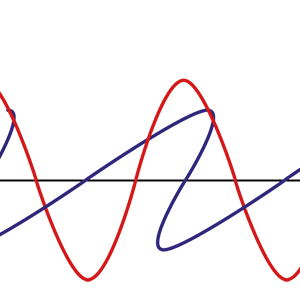
図1:偏光方向と電場の方向(磁場は電場と進行方向の両方に垂直となっています)
-
図2:検光子通過後の電場振幅の求め方
-
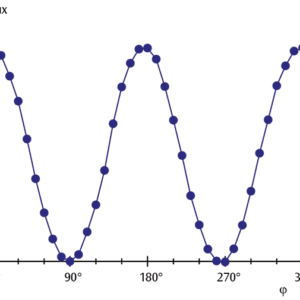
図3:検光子通過後の光強度I偏光子-検光子の角度φのグラフ
-
図4:光強度Iとcos2φのグラフ。光強度が一直線上に載っています。