磁気光学効果~ファラデー効果

実験番号:UE4040600
光学的に等方的で透明かつ非磁性の物質は,磁場中では光学的に活性になります。光の時計回りと反時計回りの円偏光成分が,物質中を通過する時間には差があるために,これらの物質は,磁場と同じ方向に透過する直線偏光した光の偏光面が回転します。この効果はファラデー効果として知られています。本実験ではファラデー効果を,フリントガラスを使って測定します。この種のガラスは非常に均一かつ大きな光の分散性を示します。その周波数の屈折率nへの依存性は,コーシーの公式によって良い近似で与えられます。
実験の手順
- フリントガラス内でのファラデー効果の発生を実証します。
- 磁場内での偏光面の回転角を測定します。
- 赤色と緑色の光に対するベルデ定数を側定します。
- 屈折率のコーシー係数bを測定します。
実験に必要な機器
- U10300:光学台,1000mm,D型 ×1
- U103111 光学台キャリア・D型,幅5cm・軸さや高9cm ×4
- U10319:光学ベース・D型 ×1
- U22000:レーザーダイオード・赤・650nm ×1
- U22001:レーザーダイオード・緑・532nm ×1
- U22017:偏光フィルター ×2
- U17130:投影スクリーン ×1
- U8497180:変圧器鉄心・D型 ×1
- U8497200:穴あき磁極片・ペア ×1
- U8497390:変圧器コイル・D 型,900巻 ×2
- U8474060:ファラデー効果実験用フリントガラスブロック ×1
- U8496420:ファラデー効果実験用アクセサリー ×1
- U855800:磁場センサー±2000mT ×1
- UCMA-BTSC1:センサー接続ケーブル ×1
- 1022284:WiLab ×1
- U13265:支柱用台座 ×1
- U13261:万能クランプ ×1
- U13255:角型ムッフ ×1
- U15002:ステンレス鋼製支柱・47cm ×1
- U13800:低電圧用リード線・75cm,15本セット ×1
- Windows PC ×1(別途ご用意ください)
実験解説書
Appendix: 円偏光とファラデー効果 ダウンロード(PDF)
基本原理
光学的に等方的で透明かつ非磁性の物質は,磁場中では光学的に活性になります。光の時計回りと反時計回りの円偏光成分が物質中を通過する時間には差があるために,これらの物質は磁場と同じ方向に透過する直線偏光した光の偏光面を回転させます。この効果はファラデー効果として知られています。
偏光が物質中を通過する際に生じる時間差は,偏光が磁場中を通過する際に生じる周波数の変化という観点から簡単なモデルを使った説明が可能です。時計回りに偏光した光は,ラーモア周波数と呼ばれる量の分だけ周波数がわずかに増加します。
(1)
反時計回りに偏光した光には,これと同量の周波数の減少が見られます。すなわち
(2)![]()
この周波数の差は物質の屈折率の違いに起因します。これは,物質内部の波の伝播速度も同様に異なることを意味します。 このことから,光学的に活性な物質内での偏光面の回転が以下のように求まります。
(3)
ラーモア周波数 fL は周波数fと比べて非常に小さいので,次の式が導出できます。
(4)
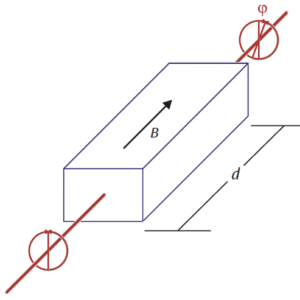
この回転角 φ は,磁場Bと光が通る物質dの長さにも比例します。
(5)![]()
この式の比例定数である,
(6)![]()
はベルデ定数と呼ばれ,光が通過する物質における光の分散とその光の周波数 f に依存します。本実験では,フリントガラス(F2)内で発生するファラデー効果の測定をします。この種のガラスは非常に均一かつ大きな光の分散性を示します。その周波数の屈折率nへの依存性は,コーシーの公式によって近似性良く与えられます。
(7)![]()
ここで,a=1.62,b=8920 nm^2
偏光の回転角が小さい場合における測定精度を向上させるために,本実験では磁場Bが正のときには,偏光解析フィルターを透過した,偏光角が0°の光の強度を弱めるように実験装置が設定されています。磁場Bが-Bに切り替えられた時には偏光解析フィルターを角度 2φ だけ回転させて,再度偏光角が0°の光の強度を減少させます。
評価
式(6)と(7)から,以下の式が導かれます。

この式は光の波長λが既知であれば,本実験で使用したフリントガラスの屈折率に対するコーシー係数bが,ベルデ定数から得られることを意味します。
![]()
参考資料
-
図1:ファラデー効果の模式図
-
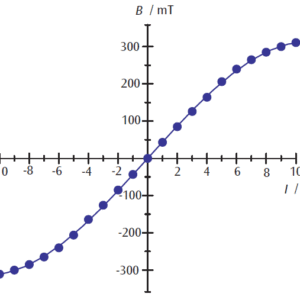
図2:電磁石の校正曲線
-
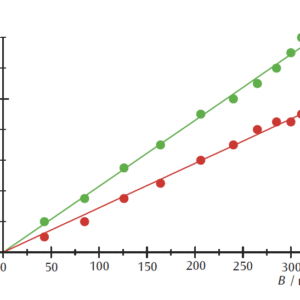
図3:赤色と緑色のレーザー光に対する,偏光の回転角と磁場との関係