ミリカンの実験
実験番号:UE5010400
ミリカンの油滴実験を通じて,電荷に最小単位(電気素量)があることを検証し,電気素量の値を測定から求めること。
実験の⼿順
- 機器のセットアップを⾏い,油滴用霧吹きのバルブを1回強く押す
- チャンバーの平板電極への電圧印加を⼊り切りし,油滴の上昇/下降時間を測定する
- 測定値から電気素量を求め,国際単位系(SI)の定義値と⽐較する
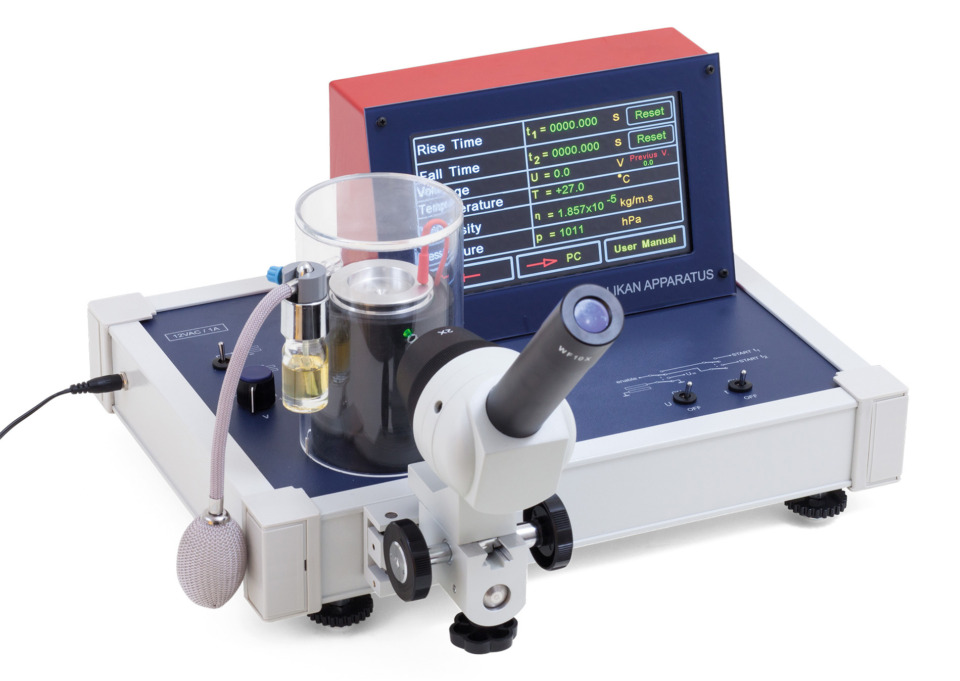
実験に必要な機器
実験解説書
基本原理
電気素量を精度良く測定したミリカンの実験を再現します。微⼩な油滴を霧吹きで作り,噴霧帯電により帯電した油滴(半径∼1μm)に電場を印加したときの移動速度と無印加での移動速度から帯電した油滴の電荷量を求めるものです。油滴の径が⼩さいためミリカンが⾏ったように空気の平均自由⾏程と油滴半径の⽐をパラメータとしてストークスの粘性抵抗式に補正を⾏います。
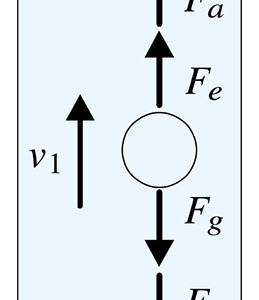
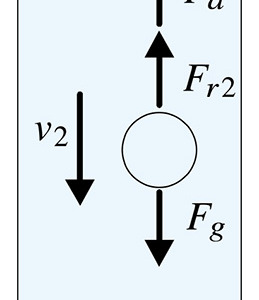
油滴はランダムに正にも負にも帯電します。そのため設定した印加電圧極性で電圧を加えたときに上昇する油滴を測定対象に取ります。実験⼿順のとおり自由落下での時間t2と電場による⼒を受けて上昇する時間t1の2つを測定します。電場による⼒を受けて上昇する速さをv1,自由落下するときの速さをv2とすればそれぞれ図1a,1bのように⼒を受け,油滴が動きだすとすぐに終端速度に逹っして⼒が釣り合った状態になっています。
図1:油滴に働く⼒
-
図1a:油滴上昇時に働く⼒
-
図1b:油滴下降時に働く⼒
- \( F_a \): 油滴に働く浮⼒
- \( F_e \): 油滴に働く静電場による⼒
- \( F_g \): 油滴に働く重⼒
- \( F_{r1} \),\( F_{r2} \):空気による粘性抵抗(ストークスの粘性抵抗)
図1に図示している⼒を具体的に書けば次の通りです。
\begin{align*} F_g &= \frac{4}{3}\pi r^3 \rho_{\mathrm{o}} g \\ F_a &= \frac{4}{3}\pi r^3 \rho_{\mathrm{a}} g \\ F_r &= 6\pi\eta r v \\ F_e &= q\frac{V}{d} \end{align*}
ここで \(\rho_{\mathrm{o}} \): 油滴の密度, \(\rho_{\mathrm{a}} \): 空気の密度,\(\eta \): 空気の粘性率,\(V \): 平⾏電極間の電圧,\(d \): 平⾏電極間隔,\(r \): 油滴を球形としたときの半径,\( v \): 油滴の速度(の大きさ)です。
図1a,1bとも⼒が釣り合っているので次の⼆式が成り⽴ちます。
(1) \begin{align*} &\frac{4}{3}\pi r^3 \rho_{\mathrm{a}} g + q\frac{V}{d} = \frac{4}{3}\pi r^3 \rho_{\mathrm{o}} g + 6\pi\eta r v_1 \\ \end{align*}
(2) \begin{align*} &\frac{4}{3}\pi r^3 \rho_{\mathrm{a}} g + 6\pi\eta r v_2 = \frac{4}{3}\pi r^3 \rho_{\mathrm{o}} g \end{align*}
(2)式から油滴の半径rが求まります。
(3) \begin{align*} r &=\sqrt{\frac{9\eta v_2}{2(\rho_{\mathrm{o}}-\rho_{\mathrm{a}})g} } \end{align*}
このrと(1)式から油滴の電荷qは次のように表せます。
(4) \begin{align*} q &= \frac{6\pi\eta d}{V}(v_1+v_2)r \end{align*}
油滴の半径が約1μm程度(表3のデータを参照)であり標準状態の空気で平均自由⾏程がおよそ0.7μmなので,ミリカンに倣ってストークスの粘性抵抗式に補正を⾏います。これは油滴の大きさがこのオーダーになると空気を⼀様な媒質とは⾒做せず,油滴と気体分⼦が「スリップ」して衝突ではなく滑るという効果が衝突の⼀部を置き換えることを意味します。
本来こうした補正を⼊れるには,別の方法で油滴の終端速度がストークスの粘性抵抗式から外れることを確認する必用があります。しかし,ここではその必要性の検討をミリカンが既に⾏っていると受け⼊れて,無条件でミリカンのストークスの粘性抵抗式への補正項を流用します。
元々のアイディアから,補正は空気の平均自由⾏程 \(\ell \)と油滴の半径 \(r \)の⽐に依存し,\(r \)が \(\ell \)に対して⼗分大きければ補正の効果は消えるとして次のようにします。
(5) \begin{align*} &F_r = \frac{6\pi\eta r v}{C} \end{align*}
(6) \begin{align*} &C=1+A\frac{\ell}{r} \end{align*}
ここで \(\ell \): 空気の平均自由⾏程,\(A \): 実験的に決定される定数です。
(5)(6)式は粘性率 \( \eta \) を \( C \)で割り補正していると⾒做せます。 \( C \)には油滴半径 \( r \)が⼊っていて,この \( r \)は補正後の \( r \)なので(5)式の \( \eta \)を \( \eta / C \)で置き換え \( r \)について解きなおします。補正した油滴半径を \( r_c \)と書けば
\begin{align*} {r_c}^2 &= \frac{9\eta v_2}{2g(\rho_{\mathrm{o}}-\rho_{\mathrm{a}})g}\frac{1}{1+A\frac{\ell}{r_c}} \end{align*}
であり,これは
(7) \begin{align*} r_c(r_c+A\ell) &= \frac{9\eta v_2}{2g(\rho_{\mathrm{o}}-\rho_{\mathrm{a}})g} \\ &= r \end{align*}
となります。(7)式右辺の \( r \)は補正前の(5)式の \( r \)です。⼆次方程式を解くだけなので \( r_c > 0 \)より
(8) \begin{align*} r_c = \sqrt{r+\frac{{A\ell}^2}{4}}-\frac{A\ell}{2} \end{align*}
となります。(8)式は次のようにも書けます。
(9) \begin{align*} r^2={r_c}^2(1+A\frac{\ell}{r_c}) \end{align*}
補正した電荷\( q_c \)は(6)式の\( \eta \)を\( \eta / C \)に,\( r \)を\( r_c \)に置き換えることで次のようになります。
(10) \begin{align*} q_c &= \frac{6\pi\eta d}{V}(v_1+v_2)r_c\left(1+A\frac{\ell}{r_c}\right)^{-3/2} \end{align*}
ここまではミリカンの議論に合わせて係数 \( A \)と平均自由⾏程 \( \ell \)を分離していましたが,メーカーでは \( A \)の値を平均自由⾏程 \( \ell \)との積で示しており次の式になるとしています。
(11) \begin{align*} A\ell &= \frac{B}{p} \end{align*}
ここで \( B \)は定数で \( B = 82 \mu m \) hPa,\( p \)は測定時の大気圧です。
実験の⼿順:
- 機器のセットアップを⾏い,内部のクリーンアップと接眼レンズの焦点をあわせる
- 接眼レンズから⾒えるマイクロメーターのどの目盛り間で油滴の移動速度を求めるか決める(目盛り間隔で2mm程度の距離)
- 油滴用霧吹きのバルブを強く1回押す(複数回押すとチャンバー内の油滴が多くなりすぎます)
- 接眼レンズでチャンバー内を観察し,適当な大きさの油滴を⾒つける
- チャンバーの平板電極に電圧を印加し,油滴が先に決めた目盛り間の上側より上に移動するように調節する
- 電圧を切り油滴が落下して上側目盛りに到達した瞬間にタイマーのスイッチ(t)をONにする(t2測定の開始)
- 油滴が下側の目盛りに到達した瞬間に印加電圧のスイッチ(U)をONにする(t2測定の終了とt1測定の開始)
- 油滴が上昇し上側の目盛りに到達したときにタイマーのスイッチ(t)をOFFにする(t1測定の終了)
- 油滴を選びなおし,別の油滴で同様にt1,t2を測定する
- 測定値から補正を⾏い電気素量を求め,国際単位系(SI)のeの定義値と⽐較する
図2:接眼レンズを通して⾒た油滴
測定
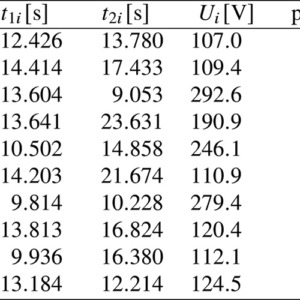
10個の油滴でそれぞれ印加電圧を変えて\( t_1 \),t2を測定しました(表1)。表1のpolarityは平⾏電極の上側電極の極性を示しています。そのためpolarity+で実験⼿順通り上へ移動する油滴は負に帯電しており,polarity-の場合は油滴は正に帯電しています。
-
表1:測定結果
-
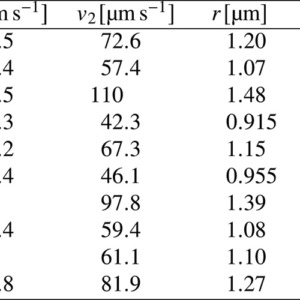
表2:補正前の油滴半径と帯電量
測定時の条件や使用したパラメータは以下の通りです。
- 平⾏電極間隔 d: 3 mm
- 油滴の移動距離 s: 1 mm
- 空気の粘性率 η: 1.88×10-5 kg/(m∙s)
- 空気の密度(25℃,1013 hPa)ρa: 1.184 kg/m3
- 油滴用オイル密度(25℃)ρo: 871 kg/m3
- 重⼒加速度 g: 9.81 m/s2
- 大気圧 p: 1014 hPa
- 補正係数 b: 82 μm hPa
- 補正係数 A=b/p: 8.09×10-8 m
これらのパラメータと(3)(4)式から補正前の値として表2のように計算しました。
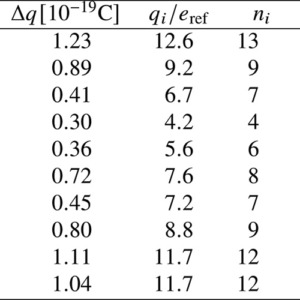
表2で求めた油滴半径\( r \)と帯電量\( q \)に(9)(10)式を使い油滴の半径が⼩さいという補正を⾏った電気素量の推定をしました。同時に(10)式から誤差伝播の式を使い帯電量の不確かさ\( Δ_q \),推定電気素量の不確かさ\( Δ_e \)も求めた結果が表3です。なお表3第4列の\( q_i / e_{ref} \)は帯電量が電気素量の何倍程度か⾒積もるために\( q_i \)を1.602×10-19で割った値です
ここで測定時の誤差(不確かさ)は次の通りです。
- 平⾏電極間距離の誤差Δd: 0.1 mm
- 接眼レンズ内スケールの誤差Δs: 50 μm
- 機器内蔵タイマーの誤差(クオーツ制御)Δt: 1 μs
- 機器内蔵電圧計の誤差(1000Vの0.5%±5ディジット)ΔV: 5.5 V
この結果を使い測定から得た電気素量の平均を求めます。この場合データのばらつきを加味する加重平均で出すのが妥当で す。重み\( w_i = (\frac{1}{\Delta e_i})^2 \)として計算します。
これから
-
表3:補正後の油滴半径rと帯電量qおよび電気素量の推定
(12) \begin{align*} e\pm\Delta e &= \frac{\sum{w_ie_i}}{\sum{w_i}}\pm\frac{1}{\sqrt{\sum{w_i}}} \\ &= (1.56\pm 0.06)\times 10^{-19} [\mathrm{C}] \end{align*}
とSI定義値 \( e = 1.602176634\times 10^{-19} [\mathrm{C}] \)と良く⼀致し,誤差範囲の中にSI定義値が⼊っています。