金属の電気伝導度

実験番号：UE3020200

金属では伝導電子が伝動機構の主役です。電気伝導度は抵抗率の逆数ですが，電場に対する伝導電子の応答という意味を持ちます。伝導電子は結晶格子の作る周期的なポテンシャルの元でほとんど自由な電子のように振る舞います。それに熱運動や不純物による散乱の影響が加わってきます。ここでは均質と見なせる2種類の金属（Al，Cu）の電気伝導度を測定します。同じく伝導電子が伝動機構の主役である金属の熱伝導（UE2020100）の結果と合わせることで，ヴィーデマン=フランツの法則も検証します。

実験の手順

• 熱伝導ロッド（Al，Cu）両端に電圧を印加し一定電流を流し，熱伝導ロッド細孔間の電位差を4端子法で測定します。
• 電流値を変えて同様の測定を繰り返します。
• 細孔間距離dと電位差Uのグラフと電流値Iと電位差Uのグラフの傾きから，それぞれの電気伝導度を求めます。
• 金属の熱伝導(UE2020100)で求めた熱伝導率と今回求めた電気伝導度からヴィーデマン=フランツの法則を検証します。

実験に必要な機器

• U8498292：アルミニウム製熱伝導ロッド ×1
• U8498291：銅製熱伝導ロッド ×1
• U8557560-115：微小信号増幅器 ×1
• U8531051：デジタルマルチメーター・E型 ×2
• U138021：プラグ付き安全リード線・75cm・15本セット ×1
• 直流電源(10V/20A) ×1 （別途ご用意ください）

お見積りフォーム

実験解説書

実験解説書 ダウンロード（PDF）

英語版 実験手順書 ダウンロード（参考，一部取り扱いのない製品も含まれています）

基本原理

金属の電気伝導の主役である伝導電子はNFEモデル（ほとんど自由な電子モデル）という金属原子の結晶格子が作る周期ポテンシャル中の電子として近似できます。これにより電気伝導度が各物質固有の物性値となります。より現実的には不純物や熱運動による散乱も考慮します。また金属の熱伝導も伝道電子による寄与が大きいことから，電気伝導度と熱伝導率は関係を持ち，これがヴィーデマン=フランツの法則となります。

長い棒状の均質な金属両端に電圧Uを印加すると，内部では一定の電場Eが生じます。その為，金属棒の長さをdとすればUとEは次の関係を満ちます。

(1)\( E=\frac { U } { d } \)

この時，流れる電流密度をjとすると電気伝導度σは電場Eと電流密度jの比例定数として定義されます。

(2)\( j=\sigma \cdot E \)

金属棒の断面積をAとすれば，流れる電流Iは(1)・（2）式から次のように書けます。

(3)\( I=j\cdot A=\sigma \cdot A\cdot \frac { U }{ d } \)

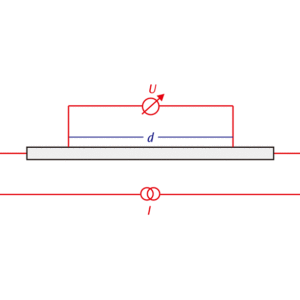
金属の電気伝導度は大きいため，測定端子の小さな接触抵抗も大きな誤差原因となりえます。これを避けるため，ここでは4端子法を用いて微小電圧を測定します。4端子法では測定回路と電流回路が独立していることから，微小電流測定用の大きなインピーダンスを持つ測定器を用いることで，測定回路にほとんど電流が流れません。これにより測定端子の接触抵抗による誤差がほぼ無視できます（図1）。

金属の熱伝導も伝導電子による寄与が大きく，電気伝導と熱伝導でキャリア（担い手）が同じである事から，何らかの関係を持つことが期待できます。その関係がヴィーデマン=フランツの法則で，温度が一定であれば，金属の電気伝導度σと熱伝導率λの比は金属によらず一定であるというものです。

(4)\( \frac {\lambda} {\sigma}=const.(\propto T) \)

実際の金属では物質によらず一定とはなりませんが，それぞれ近い値を示します。

今回測定した電気伝導度σ（Al，Cu）それぞれについてUE2020100で測定した熱伝導率λから(4)式の値を計算し比較してみましょう。

本実験は次のように行います。

1. 常温で各金属棒の両端に電圧を印加し，所望の電流値にします。基準細孔を決め，そこからの各細孔の電位差を測定します。
2. 電流値を変えて，同様の測定を行います。

評価

一定電流では(3)式より細孔間電位差Uと細孔間距離dが比例することが分かります。

\[ \sigma\cdot A\cdot \frac {U} {d}=I=const. \]

\[ \therefore U= \frac { I } { \sigma \cdot A } \cdot d,(I=const.) \]

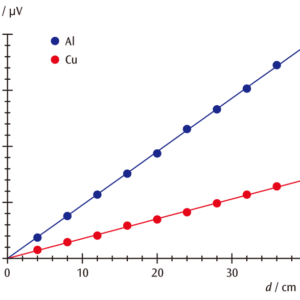
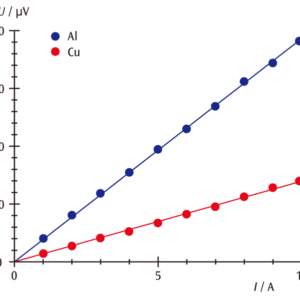
Uとdでプロットしたグラフの傾きから，Aが既知なのでσが求まります（図２）。また一定の細孔間距離で電流Iを変化させたときのUから同じようにσを求めることもできます（図３）。

\[ U= \frac { d } { \sigma \cdot A } \cdot I,(d=const.) \]

理科年表でアルミと銅の抵抗率\( ( \rho =\frac { 1 }{ \sigma } ) \)及び熱伝導率は下記のようになっています。

抵抗率\( ( 10^{-8}\Omega \cdot m ) \)

	0℃	100℃
アルミ	2.50	3.55
銅	1.55	2.23

熱伝導率\( ( \frac { W } { m \cdot K } ) \)

	0℃	100℃
アルミ	236	240
銅	403	395

測定したそれぞれの電気伝導度から，本サンプルは純粋な金属ではなく合金である事が示されます。（熱伝導ロッドはそれぞれ工業用途に使用されるAl合金・Cu合金で，カタログ掲載値はメーカーデータシートによるものです。）

参考資料