ジャイロスコープの歳差と章動

実験番号:UE1040500
コマに見られるような回転運動をしている物体に外力が働くと歳差運動(外力の向きと垂直な方向への回転運動,コマの首振り運動)が起こります。
また,回転軸が振動する章動という運動も生じます。これらの運動の力学的解析を,ジャイロスコープを用いた実験により行います。
実験の手順
- ジャイロスコープの歳差周期\(T_P\)が,回転ディスクの回転周波数\(f_R\)に比例することを確かめます。
- \(f_R\) – \(T_P\)をグラフ化し,傾きから求まる回転ディスクの慣性モーメント と,ディスクを一様な密度の剛体として計算した慣性モーメント\(I_{exp}\)を比較します。
- ジャイロスコープの章動周期 \(T_N\) が回転ディスクの回転周期\(T_R\) に比例することを確認します。
実験に必要な機器
- U52006:ジャイロスコープ実験器 ×1
- 1022284:WiLab ×1
- U11365:フォトゲート ×2
- U8557950:Connection Cable MiniDIN8 – BT ×2
- U22000:レーザーダイオード・赤・650nm ×1
- U13270:水平調整式三脚・支持穴2つ付き・15cm ×3
- U13255:角型ムッフ ×3
- U15003:ステンレス鋼製支柱・75cm ×3
- Windows PC ×1 (別途ご用意ください)
- 写真とは異なるセンサーインターフェースになります。
- Coach 7はデータ収集・解析用 PC ソフトウェアです。有効期限付きとなり,使用者数規模・有効期限長によりライセンス料金が変わります。詳しくは弊社までお問い合わせください
実験解説書
参考資料 ジャイロスコープの歳差と章動の計算 ダウンロード(PDF)
基本原理
回転運動している物体に外力が働くと,その力のモーメントにより歳差や章動と呼ばれる運動が生じます。歳差の周期は回転運動周期に反比例し,章動の周期は回転運動周期に比例します。
これらの運動は力学的に解析でき,実験結果と照らし合わせることで回転体の慣性モーメントを計算することができます。
なお,本実験の範囲では物体及び固定点と繋がる軸は,剛体として取り扱います。
1. 回転ディスクの慣性モーメント
最初に,ジャイロスコープのディスクの慣性モーメントを測定します。後に見る歳差運動から求めた慣性モーメントとも比較してみましょう。
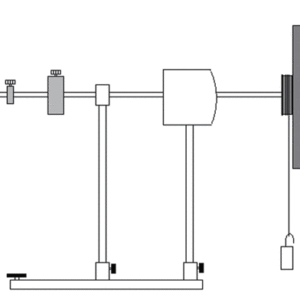
ジャイロスコープを図 1のように付属のロッドを使って軸を固定して,分銅などで一定の力のモーメント Nを与え,この時の角速度を測定します。
測定データから,次のようにディスクの慣性モーメント I を計算できます。
(1) \[ I \cdot \frac {d\omega} {dt} = N \]\[ \frac {d\omega} {dt} = const. \,\, \because I \, and \, N = const. \]\[ \therefore \,\, I \cdot \omega_E = N \cdot T_E \]
(2) \[ I = \frac {N \cdot T_E} {\omega_E} \]
ここで\(ω_E \)は測定した角速度 [rad/s] ,\(T_E \)はその時の時間 [s] です。角速度の初期値は\(0 \)としています。
また,ディスクを一様な密度 ρ の剛体とすると,慣性モーメントの定義から次のように計算することができます。
(3) \[ I = \int{\rho \cdot r^2 \cdot dV} = \rho \cdot \int{r^2 \cdot r \cdot dr \cdot d\phi \cdot dh} \]\[ = \rho \cdot 2\pi \cdot h \cdot \frac {R^4} {4} = \frac {M \cdot R^2} {2} \]\[ \because M = \rho \cdot \pi \cdot R^2 \cdot h \]
ここで,M = ディスクの質量, R = ディスクの半径,h=ディスクの厚さ,です。
測定から得た慣性モーメントと一様な密度と仮定した計算値を比較し,違いが何に起因するか検討しましょう。
2. 歳差
ジャイロスコープをディスクと反対の端に付いているおもりで軸が水平になるように調節します。
この状態ではジャイロスコープの軸(回転ディスク回転軸に一致)自身に働く重力はおもりによりキャンセルされており,一点で固定され外力が働いていない状態に等しくなります。その後,回転ディスクを回します。
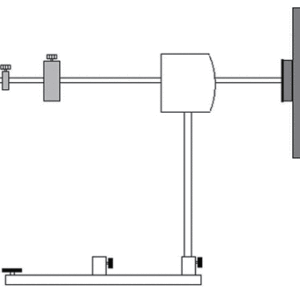
ここから小さなおもりを軸上に釣り下げ,外力を与えます(図 2 および 3 )。
この時の運動方程式を考えると次のようになります。ここで,m = 付加おもりの質量,g = 重力加速度,r =ジャイロスコープの支点から見た付加おもりを釣り下げた位置,となっています。
(4) \[ \frac {d \overrightarrow{L}} {dt} = \overrightarrow{N} =\overrightarrow{r} \times \overrightarrow{F} =\overrightarrow{r} \times \left( m \cdot g \cdot \overrightarrow{e_{重力}} \right) \]
ここで,m = 付加おもりの質量,g = 重力加速度,r = ジャイロスコープの支点から見た付加おもりを釣り下げた位置,となっています。また, \(\overrightarrow{e_{重力}} \) は重力の働く向きの単位ベクトルです。
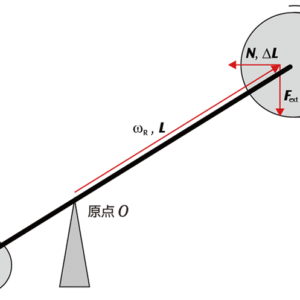
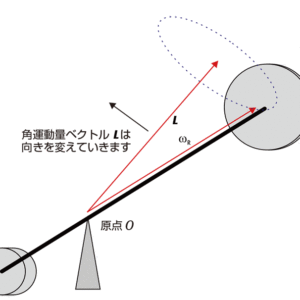
今,\(\overrightarrow{r} \)と\(\overrightarrow{e_{重力}} \)は直交しており,それらのベクトル積が角運動量L の変 化方向になります。また回転ディスクの角運動量 L の向きは\(\overrightarrow{r} \)と一致しています。よって,力のモーメントと回転ディスクの角運動量,それぞれの向きと直交する向きの回転運動が起き,これを歳差運動といいます。
運動の向きがわかったので運動方程式をスカラーとして書き直すと
(5) \[ \frac {d L} {dt} = N = m \cdot g \cdot r \]
解の導出は別紙に譲り,結果を書くと,
(6) \[ \omega_P = \frac {m \cdot g \cdot r} {I \cdot \omega_R} \]
(7) \[ \therefore T_P = \frac {4 \pi^2 \cdot I} {m \cdot g \cdot r} \cdot \frac {1} {T_R} = \frac {4 \pi^2 \cdot I} {m \cdot g \cdot r} \cdot f_R \]
となります。
ここで, \(ω_P \)= 歳差の角速度,\(ω_R \) = 回転ディスクの角速度, I = 回転ディスクの慣性モーメント, \(T_P \)= 歳差の周期,\(T_R \)= 回転ディスクの周期,\(f_R \)= 回転ディスクの振動数となります。
3. 章動
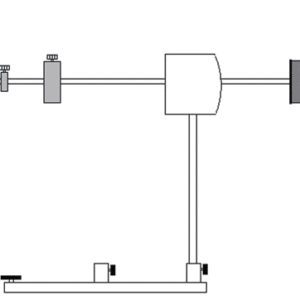
歳差運動の場合と同様に軸を水平に調整し,ディスクを回転させます。水平の向きに軽く軸を押し,固定点周りの回転運動軌道が振動することを確かめ,振動周期を測定します。
ディスクの角速度をより小さくし同様の実験を行い,振動周期を測定します。
振動周期とディスクの角速度の関係をグラフにして確認します。別紙の計算のように運動方程式から次のように章動の振動周期\(T_N \)と 回転ディスクの周期回転ディスクの周期\(T_R \)が比例することが分かります。
(8) \[ T_R = C \cdot T_N \]\[ \therefore \omega_N = C \cdot \omega_R \]
ここで, C は定数です。
4. 測定結果
4.1 歳差
次のような測定結果を得ました。
| 歳差周期\(T_p\) [s] | ディスク回転周期 \(T_R\) [s] | ディスク回転周波数\(f _R\)[Hz] |
|---|---|---|
| 16.52 | 0.08 | 12.50 |
| 15.31 | 0.09 | 11.11 |
| 14.17 | 0.10 | 10.00 |
| 12.68 | 0.11 | 9.09 |
| 11.06 | 0.12 | 8.33 |
| 10.63 | 0.13 | 7.69 |
この時,回転ディスク質量M = 1.5 [kg],回転ディスク半径R = 12.5[cm],付加おもり質量m = 150 [g],支点からのおもり釣り下げ位置r = 22.5 [cm] でした。
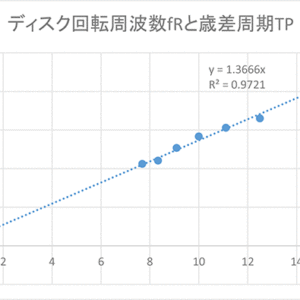
これを\(f_R \) – \(T_P \)でグラフにしたものが図6 です。グラフから歳差の周期\(T_P \)とディスクの回転周波数\(f_R \)は比例していることが分かります。近似直線が原点を通るとしたときの傾きa から求めた回転ディスクの慣性モーメント\(I_{exp} \)と(3)式から計算した\(I_{calc} \)とを比較してみます。
(9) \[ a = \frac {4 \pi^2 \cdot I_{exp}} {m \cdot g \cdot r} \]\[ I_{exp} = \frac {m \cdot g \cdot r} {4\pi^2} \cdot a \]\[ a = 1.37\text{ より,} I_{exp} = 0.0115 [kgm^2] \]\[ \text{一方,} I_{calc} = \frac {M \cdot R^2} {2} = 0.0117 [kgm^2] \]
よって,この実験では約 2 %,計算から求めた慣性モーメントと異なっていることになります。
また更に,最初に測定した回転ディスクの慣性モーメントと今回の測定を比較してみましょう。それぞれの誤差や差異が何に起因するのかを検討しましょう。
4.2 章動
次のような測定結果を得ました。
| 章動周期\(T_N\)[s] | ディスク回転周期 \(T_R\)[s] |
|---|---|
| 1.64 | 0.09 |
| 1.78 | 0.10 |
| 1.99 | 0.11 |
| 2.19 | 0.12 |
| 2.35 | 0.13 |
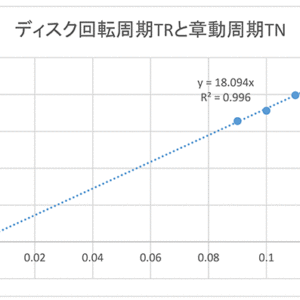
これを\(T_N \)-\(T_R \)でグラフにしたものが図7 です。グラフから章動の周期 \(T_N \)とディスクの回転周期\(T_R \)が比例していることが分かります。
比例定数Cは章動の角速度ωが小さいとしたときの近似解からは次の式となります。
(10) \[\omega’ = \frac {I_1\Omega}{I_0} \]\[ \therefore \,\,\, \frac{2\pi}{T_N} = \frac{I_1}{I_0}\frac{2\pi}{T_R} \]\[ T_N = \frac{I_0}{I_1}T_R \]
ここでω’は章動の角振動数(回転軸の上下運動の角振動数)であり, Ωはディスクの角速度,\(I_1 \)はディスクの慣性モーメント,\(I_0 \)はジャイロスコープの固定点に対する水平方向の慣性モーメントです。
ジャイロスコープの固定点に対する慣性モーメント\(I_0 \) を計算で求める事は難しいですが,ディスクの慣性モーメントよりも遥かに大きいことは,軸が長く質量を持つことより分かります。いずれにしても運動方程式から導いた「章動周期は剛体の回転周期に比例する」ということが検証できました。
参考資料
-
図1:回転ディスクの慣性モーメント測定
-
図2:歳差運動セットアップ
-
図3:歳差運動,力と角運動量の関係
-
図4:章動運動セットアップ
-
図5:章動運動概略図
-
図6:ディスク回転周波数 (f_R ) と歳差周期(T_P )
-
図7:ディスク回転周波数 \(T_R \)と歳差周期 \(T_N \)