固体中での音の伝播
実験番号：UE1070530
固体中では，音波は縦波と横波の両方で伝わります。縦波と横波は速度が異なります。これは，縦波は固体のヤング率 E に，横波はせん断弾性係数 G に依存するためです。固体中の縦波と横波の速度を測定することにより，ポアソン比 μ を含めた弾性定数を求めることができます。
実験に必要な機器
- U100102：超音波エコー像実験器 ×1
- U100151：超音波変換器・1MHz ×2
- U10020：縦波と横波の実験用音響水槽 ×1
- U10022：アルミニウム板検体・角度目盛り付き ×1
- U10026：円柱・3本セット ×1
- XP999：3B シミュレーター用潤滑剤，250ml ×1
実験解説書
基本原理
気体中や液体中では，音波は縦波でのみ伝わります。このとき，音は媒質の圧力平衡点を中心に圧力の振動を起こし，媒質の疎密の振動領域を伝えていきます（疎密波）。固体中にも音波は伝わりますが，そこでは横波も発生します。この場合，横波はせん断応力の振動が伝わるもので，固体中ではせん断応力があるために横波の音波が存在します。
縦波と横波は異なった速度となります。速度は密度 ρ と固体の弾性定数に依存し，縦波の速度cL はヤング率Eに，横波の速度 cT はせん断弾性係数Gに依存します。一般にヤング率Eはせん断弾性係数Gよりも大きいため， cL＞cTとなります。固体が一様な等方性の物質とすると，速度はそれぞれ次式で与えられます。
(1) \[ c_{L} = \sqrt{ \frac {E} {\rho} \cdot \frac {1-\mu} {( 1+ \mu ) \cdot (1 – 2\mu )} } \label{cl} \]
（2）\[c_{T} = \sqrt{ \frac {G} {\rho}}\]
また，ヤング率E，せん断弾性係数G，ポアソン比 μ の間の関係は，次のようになります。
(3) \[\frac {E} {G} = 2 \cdot (1+\mu)\]
独立な関係式が3 つあるので，cL，cT が分かれば，これら3 つの定数は計算できます。
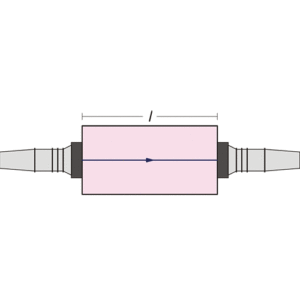
実験ではまず最初に，1MHz の超音波が長さの異なるアクリル円柱を通過する時間を測定しグラフにします。潤滑剤をつけたプローブをアクリル円柱両端にしっかりと押し付けて固定します。この状態でのプローブからの超音波はアクリル中でほとんどが縦波となります。このグラフの傾きから，アクリル中の縦波の伝播速度が分かります（図3）。
次に水槽に水を入れ，音波が水槽を通過する時間を測定します。水槽に薄いアクリルまたはアルミニウムの板を入れると，通過する時間が短 くなります。これはアクリルやアルミニウム等，固体中の音速が，水中の音速よりも速いことを示しています。
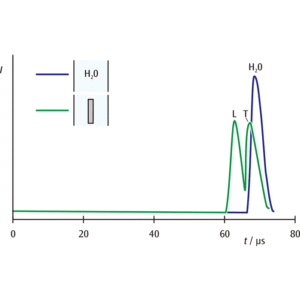
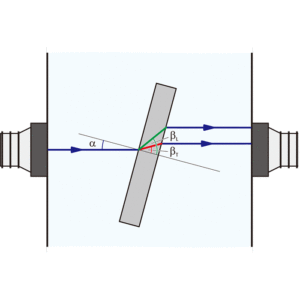
信号をよく調べると，固体の板を入れたものでは音波の到達が2 回あることが分かります（図2）。固体中では縦波と横波があるためです。 この板を傾けると，音も波なので入射角に応じて屈折します。屈折は音速に依存するので，縦波と横波で屈折角が異なります。スネルの法則より，水中の音速をc とすれば次の式が成り立ちます（図4）。
(4) \[ \frac {c} {sin{\alpha}} = \frac {c_L} {sin{\beta_L}} = \frac {c_T} {sin{\beta_T}} \]
ここで添字L,T はそれぞれ，縦波，横波の値を示しています。
固体中の縦波と横波は水中の音速よりも速いため，ある入射角で全反射が起こり，固体中に音波が侵入しない現象が起きます。この臨界角は縦波と横波で速度が異なることから，それぞれ異なり，これを測定することで，縦波と横波の速度を知ることができます。
(5) \[c_L = \frac {c} {sin{\alpha_L}}\]
(6) \[c_T = \frac {c} {\sin{\alpha_T}}\]
測定と検討
1，超音波のアクリル通過時間
測定参考図は図1を参照してください。測定結果は次のとおり でした。
表１：超音波のアクリル通過長と時間
| 円柱長l[mm] | 時間t[μs] |
|---|---|
| 40 | 15.7 |
| 80 | 30.6 |
| 120 | 45.3 |
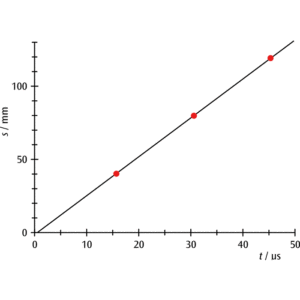
アクリル円柱での音波の通過時間を測定すると，測定点を結ぶ直線は原点を通りません（図2）。
これはプローブを通過する時間が含まれるためです（送波・受波のプローブ通過時間は同一です）。そのため，傾きからアクリル中の音速（縦波） cL を求めることができます。
上記の測定データより cL として次の値を得ました。
cL = 2660[m/s]
2，アクリルとアルミニウムの縦波・横波
表2の音速 cL と cT は測定された臨界角を式に代入することで求めました。このとき水中の音速値として，c = 1485 [m/s] を用いました。
最初にアクリル円柱を通過する時間から求めた縦波の速度 cL= 2660 [m/s] と臨界角から求めた値，cL = 2700 [m/s] が 良い一致を見せています。
1～3式を用いれば，ポアソン比 μ が次のように表せます。
(7) \[ \mu = \frac {\frac {1}{2} \cdot ( \frac {c_L}{c_T} )^2 -1} {( \frac {c_L}{c_T} )^2 -1} \]
よって密度 ρ が既知であれば， 1,2 式から，ヤング率 E とせん断弾性係数 G を計算でき，それが表 2 の値となります。
表2：アクリルとアルミニウムの縦波と横波
| アクリル | アルミニウム | |
|---|---|---|
| αL | 33° | 14° |
| sin αL | 0.54 | 0.24 |
| cL[m/s] | 2700 | 6100 |
| αT | 86° | 29° |
| sin αT | 0.998 | 0.48 |
| cT | 1500 | 3100 |
| μ | 0.29 | 0.33 |
| G[MPa] | 2700 | 25000 |
| E[MPa] | 6900 | 67000 |
| ρ[g/cm3] | 1.2 | 2.7 |
参考データ
- アルミニウム（理科年表から）
- ヤング率 E：約 70300 [MPa]
- せん断弾性係数 G：約 26100 [MPa]
アクリルは組成や加工条件から弾性係数が大きく変わるため，標準値が定まりません。
一般的なアクリル板ではヤング率 E として 2000 ～ 3000[MPa] という値が知られていますが，いずれにしてもアルミニウムより一桁小さな値となります。
参考資料
-
図1：アクリル円柱中の超音波速度測定
-
図2：水のみと板状の固体を間に入れた場合の水槽通過超音波信号
-
図3：アクリル円柱長と超音波通過時間
-
図4：固体への超音波入射角と屈折角（L：縦波，T：横波）
